题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆的上焦点
,以椭圆的上焦点![]() 为圆心,椭圆的短半轴为半径的圆与直线
为圆心,椭圆的短半轴为半径的圆与直线![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆的方程;
(2)过椭圆左顶点做两条互相垂直的直线![]() ,
,![]() ,且分别交椭圆于
,且分别交椭圆于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 不是椭圆的顶点),探究直线
不是椭圆的顶点),探究直线![]() 是否过定点,若过定点则求出定点坐标,否则说明理由.
是否过定点,若过定点则求出定点坐标,否则说明理由.
【答案】(1) ![]() (2)
(2) ![]() 恒过定点
恒过定点![]() ,见解析
,见解析
【解析】
(1)由题得![]() ,
,![]() ,解方程组即得椭圆的方程;(2)设
,解方程组即得椭圆的方程;(2)设![]() 的方程为
的方程为![]() ,
,![]() 的方程为
的方程为![]() ,当
,当![]() 斜率存在时,
斜率存在时,![]() 的方程为
的方程为![]() ,过定点
,过定点![]() ,当MN的斜率不存在时,也过定点
,当MN的斜率不存在时,也过定点![]() . 即得解.
. 即得解.
(1)∵![]() ,∴
,∴![]() ,
,
设圆![]() 的方程为
的方程为![]() ,圆心为
,圆心为![]() ,半径为
,半径为![]() ,
,
设![]() 为圆心到直线
为圆心到直线![]() 的距离,
的距离,
则![]() ,
,
∵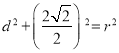 ,
,
∴![]() ,即
,即![]() ,
,
![]() ,∵
,∵![]() ,∴
,∴![]() .
.
所以椭圆的方程为![]() .
.
(2)设![]() 的方程为
的方程为![]() ,
,![]() 的方程为
的方程为![]() ,
,
联立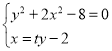 ,可得
,可得![]() ,
,
整理![]() ,设
,设![]() ,
,
∵![]() 不是椭圆的顶点,
不是椭圆的顶点,
∴![]() ,
,
代入![]() ,得
,得![]() ,
,
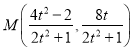 ,
,
联立 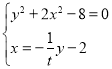 ,设
,设![]() ,
,
∴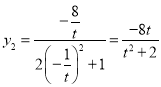 ,
,
带入![]() ,得
,得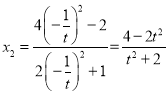 ,
,
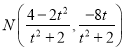 ,
,
①若![]() 斜率存在,
斜率存在,
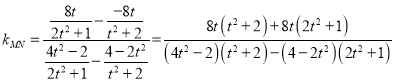
![]() ,
,
![]() :
: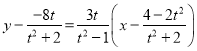
![]()

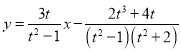
![]()
![]()
恒过![]() .
.
②若![]() 斜率不存在,
斜率不存在,
![]() 的方程为
的方程为![]() ,
,![]() 的方程为
的方程为![]() ,
,
![]() ,
,![]() ,此时
,此时![]() :
:![]() ,亦过
,亦过![]() ,
,
综上,直线![]() 恒过
恒过![]() .
.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】南方智运汽车公司在我市推出了共享汽车“Warmcar”,有一款车型为“众泰云”新能源共享汽车,其中一种租用方式“分时计费”规则为:0.15元/分钟+0.8元/公里.已知小李家离上班地点为10公里,每天租用该款汽车上、下班各一次,由于堵车、及红绿灯等原因每次路上开车花费的时间![]() (分钟)是一个随机变量,现统计了100次路上开车花费时间,在各时间段内是频数分布情况如下表所示:
(分钟)是一个随机变量,现统计了100次路上开车花费时间,在各时间段内是频数分布情况如下表所示:
时间 |
|
|
|
|
|
|
|
频数 | 2 | 6 | 14 | 36 | 28 | 10 | 4 |
(1)写出小李上班一次租车费用![]() (元)与用车时间
(元)与用车时间![]() (分钟)的函数关系;
(分钟)的函数关系;
(2)根据上面表格估计小李平均每次租车费用;
(3)“众泰云”新能源汽车还有一种租用方式为“按月计费”,规则为每个月收取租金2350元,若小李每个月上班时间平均按21天计算,在不计电费和情况下,请你为小李选择一种省钱的租车方式.
【题目】近年来,某地区积极践行“绿水青山就是金山银山”的绿色发展理念![]() 年年初至
年年初至![]() 年年初,该地区绿化面积
年年初,该地区绿化面积![]() (单位:平方公里)的数据如下表:
(单位:平方公里)的数据如下表:
年份 |
|
|
|
|
|
|
|
年份代号 |
|
|
|
|
|
|
|
绿化面积 |
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,预测该地区![]() 年年初的绿化面积,并计算
年年初的绿化面积,并计算![]() 年年初至
年年初至![]() 年年初,该地区绿化面积的年平均增长率约为多少.
年年初,该地区绿化面积的年平均增长率约为多少.
(附:回归直线的斜率与截距的最小二乘法估计公式分别为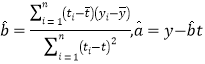 ,
,![]() )
)