题目内容
【题目】已知圆![]() :
:![]() .
.
(Ⅰ)求过点![]() 的圆
的圆![]() 的切线方程;
的切线方程;
(Ⅱ)设圆![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,点
两点,点![]() 为圆
为圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(ⅰ)当点![]() 的坐标为
的坐标为![]() 时,求以
时,求以![]() 为直径的圆的圆心坐标及半径
为直径的圆的圆心坐标及半径![]() ;
;
(ⅱ)当点![]() 在圆
在圆![]() 上运动时,以
上运动时,以![]() 为直径的圆
为直径的圆![]() 被
被![]() 轴截得的弦长是否为定值?请说明理由.
轴截得的弦长是否为定值?请说明理由.
【答案】(Ⅰ)![]() 或
或![]() ;(Ⅱ)(ⅰ)圆心为
;(Ⅱ)(ⅰ)圆心为![]() ,半径
,半径![]() ;(ⅱ)见解析
;(ⅱ)见解析
【解析】
(Ⅰ)先判断![]() 在圆
在圆![]() 外, 所以圆
外, 所以圆![]() 过点
过点![]() 的切线有两条.再由斜率是否存在分别讨论.(Ⅱ)(ⅰ)设直线PA和PB把其与直线
的切线有两条.再由斜率是否存在分别讨论.(Ⅱ)(ⅰ)设直线PA和PB把其与直线![]() 交于
交于![]() ,
,![]() 两点表示出来,写出圆的方程化简即可.(ⅱ)先求出以
两点表示出来,写出圆的方程化简即可.(ⅱ)先求出以![]() 为直径的圆
为直径的圆![]() 被
被![]() 轴截得的弦长,在设出PA和PB的直线方程,分别求出与直线
轴截得的弦长,在设出PA和PB的直线方程,分别求出与直线![]() 的交点,求出圆心,再根据勾股定理易求解.
的交点,求出圆心,再根据勾股定理易求解.
(Ⅰ)因为点![]() 在圆
在圆![]() 外, 所以圆
外, 所以圆![]() 过点
过点![]() 的切线有两条.
的切线有两条.
当直线的斜率不存在时,直线方程为![]() ,满足条件.
,满足条件.
当直线的斜率存在时,可设为![]() ,即
,即![]() .
.
由圆心到切线的距离![]() ,解得
,解得![]() . 此时切线方程为
. 此时切线方程为![]() .
.
综上,圆![]() 的切线方程为
的切线方程为![]() 或
或![]() .
.
(Ⅱ)因为圆![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,所以
两点,所以![]() ,
,![]() .
.
(ⅰ)当点![]() 坐标为
坐标为![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
直线![]() 与直线
与直线![]() 的交点坐标为
的交点坐标为![]() ,
,
同理直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
直线![]() 与直线
与直线![]() 的交点坐标为
的交点坐标为![]() . 所以以
. 所以以![]() 为直径的圆的圆心为
为直径的圆的圆心为![]() ,半径
,半径![]() .
.
(ⅱ)以![]() 为直径的圆
为直径的圆![]() 被
被![]() 轴截得的弦长为定值
轴截得的弦长为定值![]() .
.
设点![]() ,
,![]() 则
则![]() .
.
直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
直线![]() 与直线
与直线![]() 的交点坐标为
的交点坐标为![]() .
.
同理直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
直线![]() 与直线
与直线![]() 的交点坐标为
的交点坐标为![]() .
.
所以圆的圆心![]() ,半径为
,半径为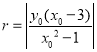 .
.
方法一:圆被![]() 轴截得的弦长为
轴截得的弦长为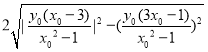
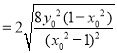
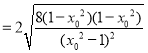
![]() .
.
所以以![]() 为直径的圆
为直径的圆![]() 被
被![]() 轴截得的弦长为定值
轴截得的弦长为定值![]() .
.
方法二:圆的方程为![]() .
.
令![]() ,解得
,解得![]()
![]()
![]()
![]() .
.
所以![]() .
.
所以圆与![]() 轴的交点坐标分别为
轴的交点坐标分别为![]() ,
,![]() .
.
所以以![]() 为直径的圆
为直径的圆![]() 被
被![]() 轴截得的弦长为定值
轴截得的弦长为定值![]() .
.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目