题目内容
15.若F1,F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,A为双曲线的左顶点,以F1,F2为直径的圆交双曲线的一条渐近线于M,N两点,且满足∠MAN=120°,则双曲线的离心率为( )| A. | $\sqrt{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{\sqrt{21}}{3}$ |
分析 首先写出圆的标准方程,画出图形,结合图形由方程组$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}={c}^{2}}\\{y=\frac{b}{a}x}\end{array}\right.$即可写出M,N两点的坐标,并且知道向量$\overrightarrow{AM},\overrightarrow{AN}$的夹角为120°,从而由cos∠MAN=$cos<\overrightarrow{AM},\overrightarrow{AN}>=-\frac{1}{2}$即可得到a,b的关系,再根据c2=a2+b2即可找到a,c的关系式,从而求出该双曲线的离心率$\frac{c}{a}$.
解答 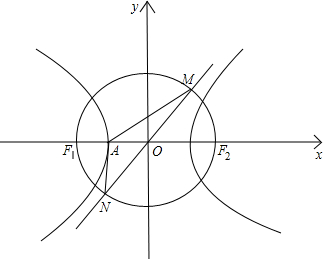 解:如图,A(a,0),由已知条件知圆的方程为:x2+y2=c2;
解:如图,A(a,0),由已知条件知圆的方程为:x2+y2=c2;
∴由$\left\{\begin{array}{l}{y=\frac{b}{a}x}\\{{x}^{2}+{y}^{2}={c}^{2}}\end{array}\right.$得:M(a,b),N(-a,-b);
∴$\overrightarrow{AM}=(0,b),\overrightarrow{AN}=(-2a,-b)$;
又∠MAN=120°;
∴$cos<\overrightarrow{AM},\overrightarrow{AN}>$=$\frac{-{b}^{2}}{\sqrt{4{a}^{2}+{b}^{2}}•b}=-\frac{1}{2}$;
∴4a2=3b2;
∴4a2=3(c2-a2);
∴7a2=3c2;
∴$\frac{c}{a}=\frac{\sqrt{21}}{3}$;
即双曲线的离心率为$\frac{\sqrt{21}}{3}$.
故选:D.
点评 考查双曲线的标准方程,双曲线焦点的概念,以及圆的标准方程,双曲线的渐近线的概念及渐近线的求法,双曲线的离心率的概念及计算公式,向量夹角余弦的坐标公式.

 正四棱锥(底面是正方形,顶点在底面上的射影是底面中心)S-ABCD的底面边长为4,高为4,点E、F、G分别为SD,CD,BC的中点,动点P在正四棱锥的表面上运动,并且总保持PG∥平面AEF,动点P的轨迹的周长为( )
正四棱锥(底面是正方形,顶点在底面上的射影是底面中心)S-ABCD的底面边长为4,高为4,点E、F、G分别为SD,CD,BC的中点,动点P在正四棱锥的表面上运动,并且总保持PG∥平面AEF,动点P的轨迹的周长为( )| A. | $\sqrt{5}$+$\sqrt{6}$ | B. | 2$\sqrt{5}$+2$\sqrt{6}$ | C. | $\sqrt{5}$+$\frac{{\sqrt{6}}}{2}$ | D. | 2$\sqrt{5}$+$\sqrt{6}$ |
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 8 |
| A. | 95 | B. | 100 | C. | 99 | D. | 90 |
| A. | y=$\sqrt{x-1}$+$\sqrt{x+1}$ | B. | y=(x-1)2 | C. | y=($\frac{1}{2}$)x-1 | D. | y=ln(x-1) |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点,F在AD上且∠FCD=30°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点,F在AD上且∠FCD=30°.