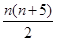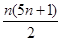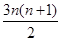题目内容
已知 是公差不等于0的等差数列,
是公差不等于0的等差数列,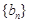 是等比数列
是等比数列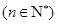 ,且
,且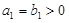 .
.
(1)若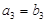 ,比较
,比较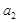 与
与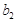 的大小关系;
的大小关系;
(2)若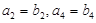 .(ⅰ)判断
.(ⅰ)判断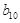 是否为数列
是否为数列 中的某一项,并请说明理由;
中的某一项,并请说明理由;
(ⅱ)若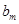 是数列
是数列 中的某一项,写出正整数
中的某一项,写出正整数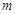 的集合(不必说明理由).
的集合(不必说明理由).
 是公差不等于0的等差数列,
是公差不等于0的等差数列,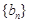 是等比数列
是等比数列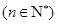 ,且
,且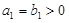 .
.(1)若
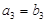 ,比较
,比较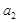 与
与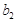 的大小关系;
的大小关系;(2)若
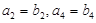 .(ⅰ)判断
.(ⅰ)判断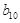 是否为数列
是否为数列 中的某一项,并请说明理由;
中的某一项,并请说明理由;(ⅱ)若
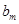 是数列
是数列 中的某一项,写出正整数
中的某一项,写出正整数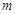 的集合(不必说明理由).
的集合(不必说明理由).(1)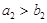 ,(2)
,(2)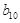 是
是 中的一项,正整数
中的一项,正整数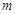 的集合是
的集合是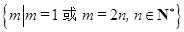 .
.
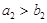 ,(2)
,(2)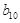 是
是 中的一项,正整数
中的一项,正整数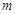 的集合是
的集合是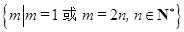 .
.试题分析:(1)记
 的
的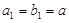 ,
, 公差为
公差为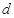 ,
,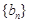 公比为
公比为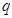 ,由
,由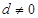 ,得
,得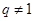 ,比较
,比较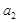 与
与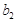 的大小关系,由已知
的大小关系,由已知 是公差不等于0的等差数列,
是公差不等于0的等差数列,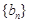 是等比数列
是等比数列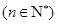 ,且
,且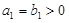 ,且
,且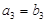 ,得
,得 ,
,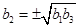 ,当
,当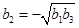 时,显然
时,显然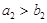 ,当
,当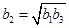 时,由平均值不等式
时,由平均值不等式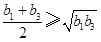 ,从而可比较
,从而可比较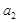 与
与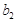 的大小关系;(2)若
的大小关系;(2)若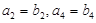 ,可得
,可得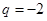 ,
,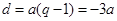 ,(ⅰ)令
,(ⅰ)令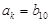 ,由等差数列,等比数列的通项公式,建立方程,解出
,由等差数列,等比数列的通项公式,建立方程,解出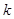 ,若是正整数,
,若是正整数,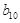 为数列
为数列 中的某一项,若不是正整数,
中的某一项,若不是正整数,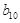 不是数列
不是数列 中的一项,(ⅱ)若
中的一项,(ⅱ)若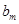 是数列
是数列 中的某一项,写出正整数
中的某一项,写出正整数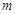 的集合,可由(ⅰ)的方法写出.
的集合,可由(ⅰ)的方法写出.试题解析:记
 的
的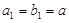 ,
, 公差为
公差为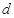 ,
,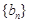 公比为
公比为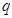 ,由
,由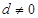 ,得
,得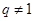
(1)
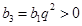 ,
, ,
,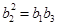 ,
,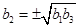 ,
,当
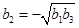 时,显然
时,显然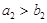 ;
;当
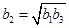 时,由平均值不等式
时,由平均值不等式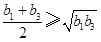 ,当且仅当
,当且仅当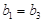 时取等号,而
时取等号,而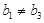 ,所以
,所以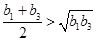 即
即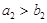 .综上所述,
.综上所述,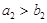 . 5分
. 5分(2)(ⅰ)因为
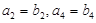 ,所以
,所以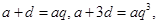 得
得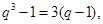 所以
所以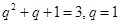 或
或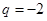 .因为
.因为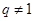 ,所以
,所以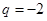 ,
,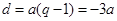 .
.令
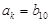 ,即
,即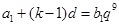 ,
,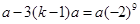 ,
,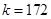 ,所以
,所以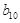 是
是 中的一项.
中的一项.(ⅱ)假设
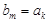 ,则
,则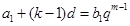 ,
,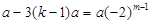 ,
,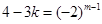
当
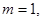 或
或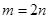 ,(
,(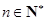 )时,
)时,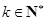 .
.正整数
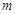 的集合是
的集合是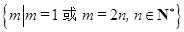 . 13分
. 13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
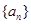 中,已知
中,已知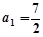 ,
,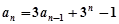 (
(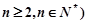 .
.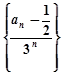 是等差数列;
是等差数列;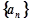 的通项公式
的通项公式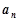 及它的前
及它的前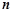 项和
项和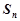 .
.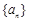 的前
的前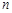 项和为
项和为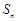 满足
满足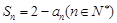 .
.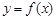 与函数
与函数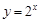 互为反函数,令
互为反函数,令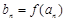 ,求数列
,求数列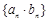 的前
的前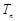 ;
;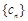 满足
满足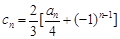 ,证明:对任意的整数
,证明:对任意的整数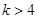 ,有
,有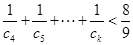 .
.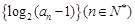 为等差数列,且
为等差数列,且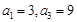 .
.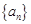 的通项公式;
的通项公式;
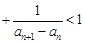 .
.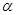 为锐角,且
为锐角,且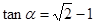 ,函数
,函数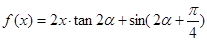 ,数列
,数列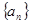 的首项
的首项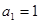 ,
,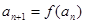 .
.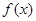 的表达式;(2)求数列
的表达式;(2)求数列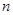 项和
项和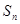 .
.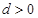 的等差数列
的等差数列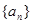 的四个命题:
的四个命题:
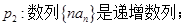

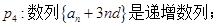




 满足
满足 ,
, ,则
,则




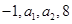 成等差数列,
成等差数列,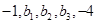 成等比数列,那么
成等比数列,那么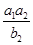 的值为( )
的值为( )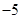
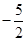
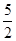
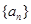 的前n项和为
的前n项和为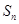 ,且
,且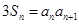 ,则
,则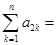 ( )
( )