Question

【题目】已知 ，方程f（x）=0有3个不同的根．
（1）求实数m的取值范围；
（2）是否存在实数m，使得f（x）在（0，1）上恰有两个极值点x1 ， x2且满足x2=2x1 ， 若存在，求实数m的值；若不存在，说明理由．

Answer 1

【答案】
（1）解：由f（x）=0得： 或ln（x2+1﹣m）=0，

可得 或 ，

方程f（x）=0有3个不同的根，

从而0＜m＜1；

（2）解：由（1）得：0＜m＜1，

f′（x）=（3x2﹣m）ln（x2+1﹣m）+ ，

令x2=t，设 ，

∴g（0）=﹣mln（1﹣m）＞0，∵0＜m＜1，

∴2﹣m＞1，∴g（1）＞0．g（a）=0，

，

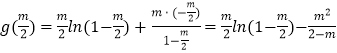∵0＜m＜1，∴g（ ）＜0

∴存在t1∈（0， ），使得g（t1）=0，另外有m∈（ ，1），使得g（a）=0

假设存在实数m，使得f（x）在（0，1）上恰有两个极值点x1，x2，且满足x2=2x1，

则存在x1∈（0， ），使得f′（x1）=0，另外有f′（ ）=0，即x2= ，

∴x1= ，∴f′（ ）=0，即（1﹣ m）ln（1﹣ m）+ m=0 （*）

设h（m）=（1﹣ m）ln（1﹣ m）+ m，

∴h′（a）=﹣ mln（1﹣ m）+ ，

∵0＜m＜1，∴h′（m）＞0，

∴h（m）在（0，1）上是增函数

∴h（m）＞h（0）=0

∴方程（*）无解，

即不存在实数m，使得f（x）在（0，1）上恰有两个极值点x1，x2，且满足x2=2x1．

【解析】（1）根据f（x）=0，得到关于m的不等式，解出m的范围即可；（2）求导数，换元，存在t1∈（0， ），使得g（t1）=0，另外有m∈（ ，1），使得g（m）=0，再利用反证法，即可得出结论．
【考点精析】通过灵活运用函数的极值与导数，掌握求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值即可以解答此题．