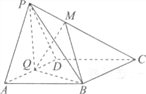
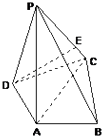
题目内容
【题目】已知椭圆![]() 上的点到它的两个焦的距离之和为
上的点到它的两个焦的距离之和为![]() ,以椭圆
,以椭圆![]() 的短轴为直径的圆
的短轴为直径的圆![]() 经过这两个焦点,点
经过这两个焦点,点![]() ,
, ![]() 分别是椭圆
分别是椭圆![]() 的左、右顶点.
的左、右顶点.
(![]() )求圆
)求圆![]() 和椭圆
和椭圆![]() 的方程.
的方程.
(![]() )已知
)已知![]() ,
, ![]() 分别是椭圆
分别是椭圆![]() 和圆
和圆![]() 上的动点(
上的动点(![]() ,
, ![]() 位于
位于![]() 轴两侧),且直线
轴两侧),且直线![]() 与
与![]() 轴平行,直线
轴平行,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .求证:
.求证: ![]() 为定值.
为定值.
【答案】(![]() )
)![]() ;
; ![]() ;(
;(![]() )见解析.
)见解析.
【解析】试题分析:
(1)根据椭圆定义知![]() ,又
,又![]() ,因此易求得
,因此易求得![]() ,得椭圆方程,从而也得到圆的方程;
,得椭圆方程,从而也得到圆的方程;
(2)设出![]() ,
, ![]() ,分别代入椭圆方程和圆的方程得到两个关系式,写出直线AP的方程,求出M点坐标,同理写出BP方程,求出N点坐标,再求得向量
,分别代入椭圆方程和圆的方程得到两个关系式,写出直线AP的方程,求出M点坐标,同理写出BP方程,求出N点坐标,再求得向量![]() ,并计算数量积
,并计算数量积![]() ,结果为0,可得
,结果为0,可得![]() .
.
试题解析:
(![]() )依题意
)依题意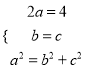 ,得
,得![]() ,
, ![]() ,
,
∴圆方程![]() ,椭圆
,椭圆![]() 方程
方程![]() .
.
(![]() )设
)设![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∵![]() 方程
方程![]() ,令
,令![]() 时,
时, 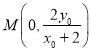 ,
,
![]() 方程为
方程为![]() ,令
,令![]() 得
得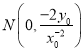 ,
,
∴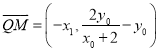 ,
, 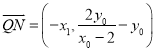 ,
,
∴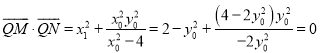 ,
,
∴![]() .
.

练习册系列答案
相关题目