题目内容
14.对于函数f(x)=aex+x,若存在实数m,n,使得f(x)≥0的解集为[m,n](m<n),则实数a的取值范围是( )| A. | (-$\frac{1}{e}$,0)∪(0,+∞) | B. | [-$\frac{1}{e}$)∪(0,+∞) | C. | (-$\frac{1}{e}$,0) | D. | [-$\frac{1}{e}$,0) |
分析 将f(x)≥0转化aex≥-x,进而转化为a的不等式,求出表达式的最大值,以及单调区间,即可得到a的取值范围.
解答 解:若f(x)≥0,则aex≥-x(e是自然对数的底数),
转化为a≥$-\frac{x}{{e}^{x}}$,
令y=$-\frac{x}{{e}^{x}}$,
则y′=$\frac{(x-1)}{{e}^{x}}$,
令y′=0,可得x=1,
当x>1时,y′>0,函数y递增;当x<1时,y′<0,函数y递减.
则当x=1时,函数y取得最小值-$\frac{1}{e}$,
由于存在实数m、n,使得f(x)≥0的解集为[m,n],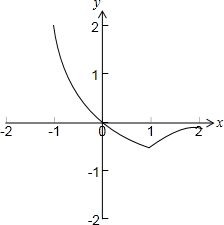
则由函数y=$-\frac{x}{{e}^{x}}$的图象可得a的取值范围为(-$\frac{1}{e}$,0),
故选:C.
点评 本题考查函数的导数的最值的应用,考查转化思想与计算能力.

练习册系列答案
相关题目
5.在下列各图中,图中两个变量具有相关关系的图是( )
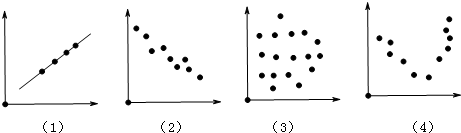

| A. | (1)(2) | B. | (1)(4) | C. | (2)(4) | D. | (2)(3) |
4.曲线y=cosx(0≤x≤$\frac{3π}{2}$)与x轴以及直线x=$\frac{3π}{2}$所围图形的面积为( )
| A. | 4 | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
 如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1km.求B,D的距离$\frac{{3\sqrt{2}+\sqrt{6}}}{20}$.
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1km.求B,D的距离$\frac{{3\sqrt{2}+\sqrt{6}}}{20}$.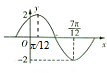 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图,求:
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤π),在一个周期内的图象如图,求: