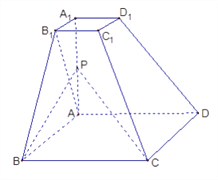
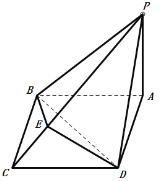
题目内容
【题目】已知数列![]() 是无穷数列,满足
是无穷数列,满足![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)求证:“数列![]() 中存在
中存在![]() 使得
使得![]() ”是“数列
”是“数列![]() 中有无数多项是
中有无数多项是![]() ”的充要条件;
”的充要条件;
(3)求证:在数列![]() 中
中![]() ,使得
,使得![]() .
.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】
(1)由![]() ,
,![]() ,结合
,结合![]() 可得
可得![]() 、
、![]() 、
、![]() 的值;
的值;
(2)分必要性和充分性证明,充分性利用反证法证明;
(3)利用反证法,假设数列![]() 中不存在
中不存在![]() ,使得
,使得![]() ,则
,则![]() 或
或![]() ,然后分类推出矛盾得答案.
,然后分类推出矛盾得答案.
(1)![]() ,
,![]() ,
,![]() ,
,
![]() ,则
,则![]() ;
;
![]() ,则
,则![]() ;
;
![]() ,则
,则![]() .
.
因此,![]() ,
,![]() ,
,![]()
(2)必要性:已知数列![]() 中有无数多项是
中有无数多项是![]() ,
,
则数列![]() 中存在
中存在![]() 使得
使得![]() .
.
![]() 数列
数列![]() 中有无数多项是
中有无数多项是![]() ,
,![]() 数列
数列![]() 中存在
中存在![]() 使得
使得![]() ,
,
即数列![]() 中存在
中存在![]() 使得
使得![]() ;
;
充分性:已知数列![]() 中存在
中存在![]() 使得
使得![]() ,则数列
,则数列![]() 中有无数多项是
中有无数多项是![]() .
.
假设数列![]() 中没有无数多项是
中没有无数多项是![]() ,不妨设
,不妨设![]() 是数列
是数列![]() 中为
中为![]() 的最后一项,则
的最后一项,则![]() ,若
,若![]() ,
,
则由![]() ,可得
,可得![]() ,
,
![]() ,则
,则![]() ,与假设矛盾;
,与假设矛盾;
若![]() ,则由
,则由![]() ,可得
,可得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,得
,得![]() ,与假设矛盾,原命题正确.
,与假设矛盾,原命题正确.
由上可知,“数列![]() 中存在
中存在![]() 使得
使得![]() ”是“数列
”是“数列![]() 中有无数多项是
中有无数多项是![]() ”的充要条件;
”的充要条件;
(3)假设数列![]() 中不存在
中不存在![]() ,使得
,使得![]() ,
,
则![]() 或
或![]() ,由
,由![]() ,
,
可得
![]() ①,且
①,且![]() ,
,
当![]() 时,
时,![]() ,由假设知
,由假设知![]() .
.
若![]() ,则
,则![]() ,与
,与![]() 矛盾;
矛盾;
若![]() ,设
,设![]() ,则
,则![]() ,
,
由①可得![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,![]() ,
,
对于![]() ,显然存在
,显然存在![]() 使得
使得![]() ,
,![]() ,这与
,这与![]() 矛盾.
矛盾.
所以,假设不成立,原命题正确.

【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: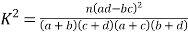
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |