题目内容
【题目】已知![]() 的内角A,B,C所对的边分别是a,b,c,其面积S
的内角A,B,C所对的边分别是a,b,c,其面积S![]() .
.
(1)若a![]() ,b
,b![]() ,求cosB.
,求cosB.
(2)求sin(A+B)+sinBcosB+cos(B﹣A)的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据面积S![]() 结合面积公式和余弦定理化简可得
结合面积公式和余弦定理化简可得![]() ,解得
,解得 ![]() ,然后根据a
,然后根据a![]() ,b
,b![]() ,由正弦定理求得
,由正弦定理求得![]() ,再利用平方关系求解.
,再利用平方关系求解.
(2)由(1)知![]() ,sin(A+B)+sinBcosB+cos(B﹣A),可化为
,sin(A+B)+sinBcosB+cos(B﹣A),可化为![]() , 令
, 令![]() ,转化为二次函数求解.
,转化为二次函数求解.
(1)因为三角形面积为S![]() ,
,
所以![]() ,
,
解得 ![]() ,
,
因为a![]() ,b
,b![]() ,
,
由正弦定理得:![]() ,
,
所以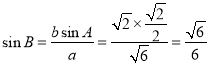 ,
,
因为![]() ,
,
所以![]() ,
,
所以![]() 为锐角,
为锐角,
所以![]()
(2)由(1)知![]() ,
,
所以sin(A+B)+sinBcosB+cos(B﹣A),
![]() ,
,
![]() ,
,![]() ,
,
令![]() ,
,
因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
原式![]() ,
,
当![]() 时,原式取得最大值
时,原式取得最大值![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】惠州市某学校高三年级模拟考试的数学试题是全国I卷的题型结构,其中第22、23题为选做题,考生只需从中任选一题作答.已知文科数学和理科数学的选做题题目无任何差异,该校参加模拟考试学生共1050人,其中文科学生150人,理科学生900人.在测试结束后,数学老师对该学校全体高三学生选做的22题和23题得分情况进行了统计,22题统计结果如下表1,23题统计结果如下表2.
表1
22题得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 50 | 70 | 80 | 100 | 500 |
文科人数 | 5 | 20 | 10 | 5 | 70 |
表2
23题得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 10 | 10 | 15 | 25 | 40 |
文科人数 | 5 | 5 | 25 | 0 | 5 |
(1)在答卷中完成如下![]() 列联表,并判断能否至少有
列联表,并判断能否至少有![]() 的把握认为“选做22题或23题”与“学生的科类(文理)”有关系;
的把握认为“选做22题或23题”与“学生的科类(文理)”有关系;
选做22题 | 选做23题 | 合计 | |
文科人数 | 110 | ||
理科人数 | 100 | ||
总计 | 1050 |
(2)在第23题得分为0的学生中,按分层抽样的方法随机抽取6人进行答疑辅导,并在辅导后从这6人中随机抽取2人进行测试,求被抽中进行测试的2名学生均为理科生的概率.
参考公式: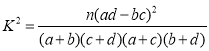 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 | A | B | C | D |
频数 | 40 | 20 | 20 | 20 |
乙分厂产品等级的频数分布表
等级 | A | B | C | D |
频数 | 28 | 17 | 34 | 21 |
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?