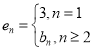题目内容
【题目】已知抛物线![]() 和点D(2,0),直线
和点D(2,0),直线 ![]() 与抛物线C交于不同两点A、B,直线BD与抛物线C交于另一点E.给出以下判断:
与抛物线C交于不同两点A、B,直线BD与抛物线C交于另一点E.给出以下判断:
①直线OB与直线OE的斜率乘积为-2; ②![]() 轴; ③以BE为直径的圆与抛物线准线相切;
轴; ③以BE为直径的圆与抛物线准线相切;
其中,所有正确判断的序号是( )
A.①②③B.①②C.①③D.②③
【答案】B
【解析】
由题意,可设直线![]() 的方程为
的方程为![]() ,利用韦达定理判断第一个结论;将
,利用韦达定理判断第一个结论;将![]() 代入抛物线
代入抛物线![]() 的方程可得,
的方程可得,![]() ,从而,
,从而,![]() ,进而判断第二个结论;设
,进而判断第二个结论;设![]() 为抛物线
为抛物线![]() 的焦点,以线段
的焦点,以线段![]() 为直径的圆为
为直径的圆为![]() ,则圆心
,则圆心![]() 为线段
为线段![]() 的中点.设
的中点.设![]() ,
,![]() 到准线的距离分别为
到准线的距离分别为![]() ,
,![]() ,
,![]() 的半径为
的半径为![]() ,点
,点![]() 到准线的距离为
到准线的距离为![]() ,显然
,显然![]() ,
,![]() ,
,![]() 三点不共线,进而判断第三个结论.
三点不共线,进而判断第三个结论.
解:由题意,可设直线![]() 的方程为
的方程为![]() ,
,
代入抛物线![]() 的方程,有
的方程,有![]() .
.
设点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
所![]() .
.
则直线![]() 与直线
与直线![]() 的斜率乘积为
的斜率乘积为![]() .所以①正确.
.所以①正确.
将![]() 代入抛物线
代入抛物线![]() 的方程可得,
的方程可得,![]() ,从而,
,从而,![]() ,
,
根据抛物线的对称性可知,![]() ,
,![]() 两点关于
两点关于![]() 轴对称,
轴对称,
所以直线![]() 轴.所以②正确.
轴.所以②正确.
如图,设![]() 为抛物线
为抛物线![]() 的焦点,以线段
的焦点,以线段![]() 为直径的圆为
为直径的圆为![]() ,
,
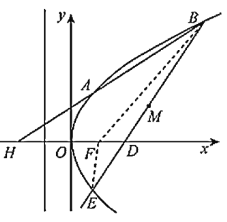
则圆心![]() 为线段
为线段![]() 的中点.设
的中点.设![]() ,
,![]() 到准线的距离分别为
到准线的距离分别为![]() ,
,![]() ,
,![]() 的半径为
的半径为![]() ,点
,点![]() 到准线的距离为
到准线的距离为![]() ,显然
,显然![]() ,
,![]() ,
,![]() 三点不共线,
三点不共线,
则![]() .所以③不正确.
.所以③不正确.
故选:B.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目