题目内容
【题目】已知直线![]() 过定点
过定点![]() ,圆
,圆![]() .在圆
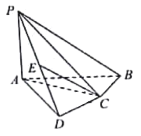
.在圆![]() 上任取一点P,连接
上任取一点P,连接![]() ,在
,在![]() 上取点M,使得
上取点M,使得![]() 是以
是以![]() 为底的等腰三角形.
为底的等腰三角形.
(1)求点M的轨迹方程;
(2)过点![]() 的直线
的直线![]() 与点M的轨迹交于A,B两点,O为坐标原点,求
与点M的轨迹交于A,B两点,O为坐标原点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)确定直线过定点![]() ,再根据圆的几何意义和椭圆的定义,即可得点M的轨迹为椭圆,写出其标准方程即可;(2)设出直线
,再根据圆的几何意义和椭圆的定义,即可得点M的轨迹为椭圆,写出其标准方程即可;(2)设出直线![]() 的方程,与椭圆的方程联立,根据根与系数的关系,求出
的方程,与椭圆的方程联立,根据根与系数的关系,求出![]() 面积的表达式,通过换元,利用基本不等式求出最值即可.
面积的表达式,通过换元,利用基本不等式求出最值即可.
解:(1)直线![]() ,变形为
,变形为![]() ,
,
∴直线l过定点![]() ,圆
,圆![]() ,
,
变形为![]() ,可知圆心
,可知圆心![]() ,半径
,半径![]() .
.
∵![]() 是以
是以![]() 为底的等腰三角形,∴
为底的等腰三角形,∴![]() ,
,
则![]() ,
,
可知点M的轨迹为以点![]() 为焦点,4为长轴长的椭圆,
为焦点,4为长轴长的椭圆,
∴![]() ,
,
∴点M的轨迹方程为![]() .
.
(2)设直线![]() ,点
,点![]() ,
,
联立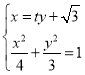 ,得
,得![]() ,
,
显然![]() ,
,
∴![]() ,
,
∴![]()
![]()
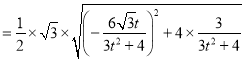
![]() ,
,
∵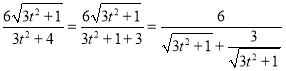 ,
,
设![]() ,
,
∴![]() ,
,
∴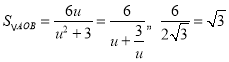 ,
,
当且仅当![]() 时等号成立,故
时等号成立,故![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
相关题目
【题目】下表为2016年至2019年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 | 1 | 2 | 3 | 4 |
线下销售额 | 95 | 165 | 230 | 310 |
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测2020年该百货零售企业的线下销售额;
的线性回归方程,并预测2020年该百货零售企业的线下销售额;
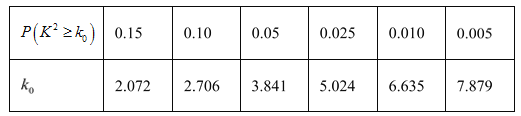
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了55位男顾客、50位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有10人、女顾客有20人,能否在犯错误的概率不超过0.025的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据:
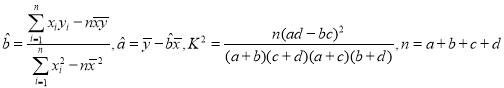 .
.