题目内容
在直角坐标系xOy中,曲线C1的点均在C2:(x-5)2+y2=9外,且对C1上任意一点M,M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值.
(Ⅰ)求曲线C1的方程;
(1-4班做)(Ⅱ)设P(x0,y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值.
(5-7班做)(Ⅱ)设P(-4,1)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D.证明:四点A,B,C,D的纵坐标之积为定值.
(Ⅰ)求曲线C1的方程;
(1-4班做)(Ⅱ)设P(x0,y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值.
(5-7班做)(Ⅱ)设P(-4,1)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D.证明:四点A,B,C,D的纵坐标之积为定值.
(Ⅰ)曲线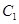 的方程为
的方程为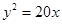 .
.
(Ⅱ)当P在直线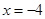 上运动时,四点A,B,C,D的纵坐标之积为定值6400.
上运动时,四点A,B,C,D的纵坐标之积为定值6400.
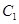 的方程为
的方程为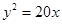 .
.(Ⅱ)当P在直线
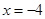 上运动时,四点A,B,C,D的纵坐标之积为定值6400.
上运动时,四点A,B,C,D的纵坐标之积为定值6400.本事试题主要是考查了解析几何中运用坐标法解决几何问题的实质。
(1)由题设知,曲线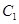 上任意一点M到圆心
上任意一点M到圆心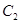
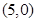 的距离等于它到直线
的距离等于它到直线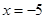 的距离,因此,曲线
的距离,因此,曲线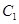 是以
是以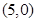 为焦点,直线
为焦点,直线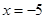 为准线的抛物线,故其方程为
为准线的抛物线,故其方程为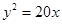
(2)因为P的坐标为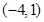 ,则过P且与圆
,则过P且与圆
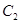 相切得直线的斜率
相切得直线的斜率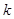 存在且不为0,每条切线都与抛物线有两个交点,切线方程为
存在且不为0,每条切线都与抛物线有两个交点,切线方程为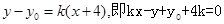 ,
,
设过P所作的两条切线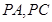 的斜率分别为
的斜率分别为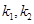 ,则
,则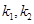 是方程①的两个实根,故
是方程①的两个实根,故
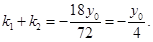 同理得到
同理得到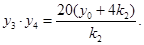 ,进而证明。
,进而证明。
(2)当点P在直线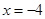 上运动时,P的坐标为
上运动时,P的坐标为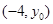 ,又
,又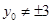 ,则过P且与圆
,则过P且与圆
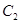 相切得直线的斜率
相切得直线的斜率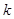 存在且不为0,每条切线都与抛物线有两个交点,切线方程为
存在且不为0,每条切线都与抛物线有两个交点,切线方程为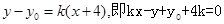 ,
,
设过P所作的两条切线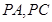 的斜率分别为
的斜率分别为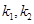 ,则
,则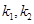 是方程①的两个实根,故
是方程①的两个实根,故
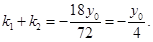 同理得到
同理得到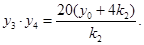 ,进而证明。
,进而证明。
(1)由题设知,曲线
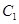 上任意一点M到圆心
上任意一点M到圆心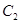
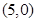 的距离等于它到直线
的距离等于它到直线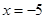 的距离,因此,曲线
的距离,因此,曲线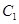 是以
是以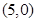 为焦点,直线
为焦点,直线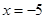 为准线的抛物线,故其方程为
为准线的抛物线,故其方程为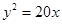
(2)因为P的坐标为
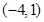 ,则过P且与圆
,则过P且与圆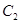 相切得直线的斜率
相切得直线的斜率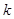 存在且不为0,每条切线都与抛物线有两个交点,切线方程为
存在且不为0,每条切线都与抛物线有两个交点,切线方程为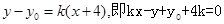 ,
,设过P所作的两条切线
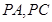 的斜率分别为
的斜率分别为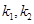 ,则
,则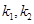 是方程①的两个实根,故
是方程①的两个实根,故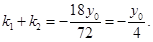 同理得到
同理得到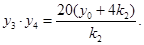 ,进而证明。
,进而证明。(2)当点P在直线
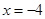 上运动时,P的坐标为
上运动时,P的坐标为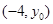 ,又
,又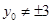 ,则过P且与圆
,则过P且与圆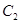 相切得直线的斜率
相切得直线的斜率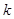 存在且不为0,每条切线都与抛物线有两个交点,切线方程为
存在且不为0,每条切线都与抛物线有两个交点,切线方程为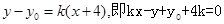 ,
,设过P所作的两条切线
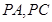 的斜率分别为
的斜率分别为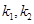 ,则
,则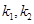 是方程①的两个实根,故
是方程①的两个实根,故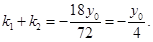 同理得到
同理得到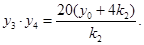 ,进而证明。
,进而证明。
练习册系列答案
相关题目
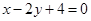 与直线
与直线 的交点,且与点A(0,4)和点B(4,O)距离相等的直线方程.
的交点,且与点A(0,4)和点B(4,O)距离相等的直线方程.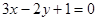 和直线
和直线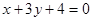 的交点,且垂直于直线
的交点,且垂直于直线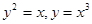 围成的封闭图形面积为____.
围成的封闭图形面积为____.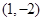 ,且过点
,且过点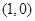 ,该直线的方程为
,该直线的方程为 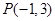 关于直线
关于直线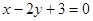 的对称点Q的坐标为________.
的对称点Q的坐标为________. ,若直线PA的方程为
,若直线PA的方程为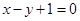 ,则直线PB的方程是( )
,则直线PB的方程是( )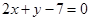 B.
B. 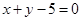
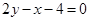 D.
D. 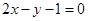
 ,且满足下列条件的直线方程:
,且满足下列条件的直线方程: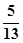 ; (2)与两坐标轴的正半轴围成的三角形面积为4。
; (2)与两坐标轴的正半轴围成的三角形面积为4。