题目内容
数列 的通项公式
的通项公式 ,其前
,其前 项和为
项和为 ,则
,则 等于
等于
 的通项公式
的通项公式 ,其前
,其前 项和为
项和为 ,则
,则 等于
等于 1006
因为 ,那么周期为4的函数,那么
,那么周期为4的函数,那么
∴a1+a2+a3+a4=(0-2+0+4)=2,a5+a6+a7+a8=(0-6+0+8)=2,,…,a2009+a2010+a2011+a2012=(0-2010+0+2012)=2,,S2012=a1+a2+a3+a4+…+a2012,=(0-2+0+4)+(0-6+0+8)+…+(0-2010+0+2012),=2×503=1006,故填写1006
 ,那么周期为4的函数,那么
,那么周期为4的函数,那么∴a1+a2+a3+a4=(0-2+0+4)=2,a5+a6+a7+a8=(0-6+0+8)=2,,…,a2009+a2010+a2011+a2012=(0-2010+0+2012)=2,,S2012=a1+a2+a3+a4+…+a2012,=(0-2+0+4)+(0-6+0+8)+…+(0-2010+0+2012),=2×503=1006,故填写1006

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

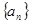 的通项公式为
的通项公式为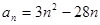 ,则数列
,则数列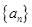 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为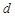 ,
,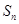 为其前
为其前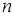 项和,且满足
项和,且满足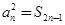 ,
,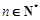 .数列
.数列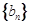 满足
满足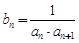 ,
,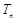 为数列
为数列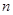 项和.
项和.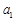 、
、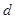 和
和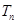 ;
;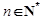 ,不等式
,不等式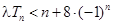 恒成立,求实数
恒成立,求实数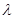 的取值范围;
的取值范围;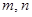
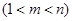 ,使得
,使得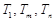 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有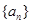 ,
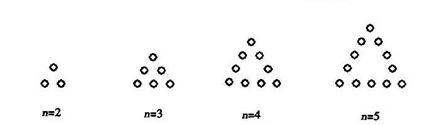
,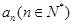 对应图中星星的个数.
对应图中星星的个数.
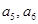 的值及数列
的值及数列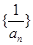 的前n项和
的前n项和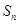 ;
;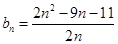 ,对于(2)中的
,对于(2)中的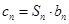 ,求数列
,求数列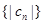 的前n项和
的前n项和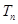 ;
; ,则
,则 = .
= . 个点,每个图形总的点数记为
个点,每个图形总的点数记为 ,则
,则 ( )
( )




 满足
满足 则
则 的最小值为
的最小值为