题目内容
(本小题满分14分)已知数列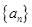 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为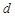 ,
,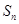 为其前
为其前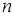 项和,且满足
项和,且满足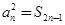 ,
,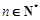 .数列
.数列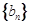 满足
满足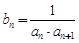 ,
,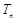 为数列
为数列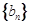 的前
的前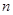 项和.
项和.
(1)求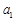 、
、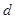 和
和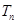 ;
;
(2)若对任意的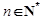 ,不等式
,不等式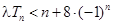 恒成立,求实数
恒成立,求实数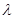 的取值范围;
的取值范围;
(3)是否存在正整数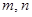
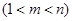 ,使得
,使得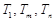 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有
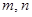 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
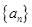 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为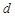 ,
,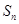 为其前
为其前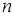 项和,且满足
项和,且满足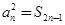 ,
,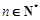 .数列
.数列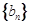 满足
满足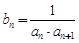 ,
,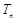 为数列
为数列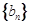 的前
的前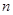 项和.
项和.(1)求
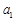 、
、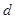 和
和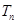 ;
;(2)若对任意的
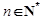 ,不等式
,不等式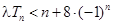 恒成立,求实数
恒成立,求实数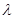 的取值范围;
的取值范围;(3)是否存在正整数
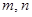
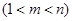 ,使得
,使得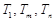 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有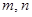 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. (1)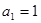 ,
,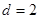 ,
,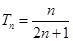 .
.
(2)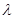 的取值范围是
的取值范围是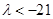 .
.
(3)当且仅当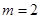 ,
, 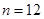 时,数列
时,数列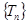 中的
中的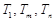 成等比数列.
成等比数列.
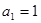 ,
,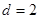 ,
,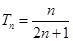 .
. (2)
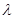 的取值范围是
的取值范围是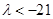 .
. (3)当且仅当
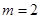 ,
, 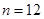 时,数列
时,数列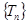 中的
中的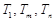 成等比数列.
成等比数列. 本试题主要是考查了数列通项公式与前n项和之间的关系的运用以及分类讨论思想求解最值。
(1)利用 an2=S2n-1,n取1或2,可求数列的首项与公差,从人体可得数列的通项,进而可求数列的和;
(2)分类讨论,分离参数,求出对应函数的最值,即可求得结论.
(3)根据已知值成等比数列,可知参数m的范围,然后利用m是整数,得到值。
解:(1)(法一)在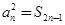 中,令
中,令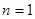 ,
,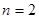 ,
,
得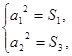 即
即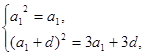 ………………………2分
………………………2分
解得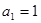 ,
,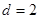 , …………………3分
, …………………3分
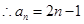 .
.
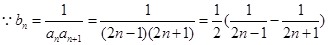 ,
,
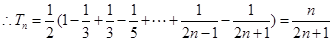 . ……………………5分
. ……………………5分
(法二)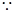
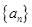 是等差数列,
是等差数列, 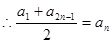
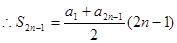
 . …………………………2分
. …………………………2分
由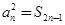 ,得
,得 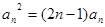 ,
,
又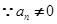 ,
,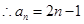 ,则
,则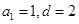 . …………………3分
. …………………3分
(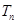 求法同法一)
求法同法一)
(2)①当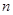 为偶数时,要使不等式
为偶数时,要使不等式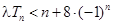 恒成立,即需不等式
恒成立,即需不等式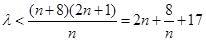 恒成立. …………………………………6分
恒成立. …………………………………6分
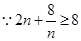 ,等号在
,等号在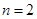 时取得.
时取得.
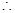 此时
此时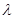 需满足
需满足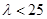 . …………………………7分
. …………………………7分
②当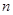 为奇数时,要使不等式
为奇数时,要使不等式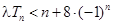 恒成立,即需不等式
恒成立,即需不等式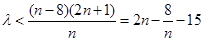 恒成立. ……………………………8分
恒成立. ……………………………8分
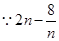 是随
是随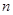 的增大而增大,
的增大而增大, 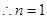 时
时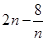 取得最小值
取得最小值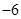 .
.
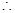 此时
此时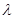 需满足
需满足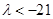 . …………………………9分
. …………………………9分
综合①、②可得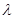 的取值范围是
的取值范围是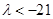 . …………………………10分
. …………………………10分
(3)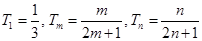 ,
,
若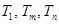 成等比数列,则
成等比数列,则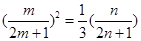 ,即
,即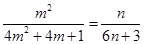 .11分
.11分
(法一)由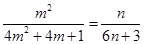 , 可得
, 可得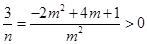 ,
,
即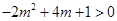 , ……………………12分
, ……………………12分
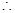
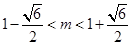 . ……………………13分
. ……………………13分
又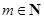 ,且
,且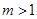 ,所以
,所以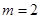 ,此时
,此时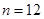 .
.
因此,当且仅当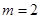 ,
, 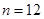 时,数列
时,数列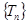 中的
中的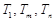 成等比数列.…………14分
成等比数列.…………14分
(法二)因为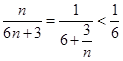 ,故
,故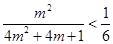 ,即
,即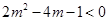 ,
,
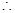
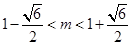 ,(以下同上).…………………13分
,(以下同上).…………………13分
(1)利用 an2=S2n-1,n取1或2,可求数列的首项与公差,从人体可得数列的通项,进而可求数列的和;
(2)分类讨论,分离参数,求出对应函数的最值,即可求得结论.
(3)根据已知值成等比数列,可知参数m的范围,然后利用m是整数,得到值。
解:(1)(法一)在
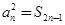 中,令
中,令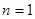 ,
,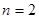 ,
,得
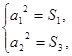 即
即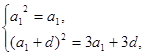 ………………………2分
………………………2分解得
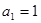 ,
,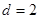 , …………………3分
, …………………3分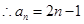 .
.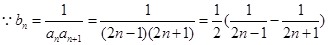 ,
,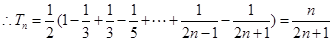 . ……………………5分
. ……………………5分(法二)
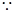
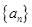 是等差数列,
是等差数列, 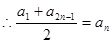
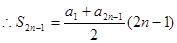
 . …………………………2分
. …………………………2分由
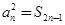 ,得
,得 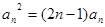 ,
, 又
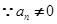 ,
,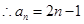 ,则
,则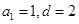 . …………………3分
. …………………3分(
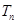 求法同法一)
求法同法一)(2)①当
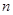 为偶数时,要使不等式
为偶数时,要使不等式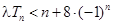 恒成立,即需不等式
恒成立,即需不等式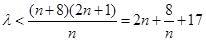 恒成立. …………………………………6分
恒成立. …………………………………6分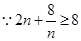 ,等号在
,等号在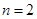 时取得.
时取得. 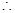 此时
此时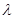 需满足
需满足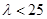 . …………………………7分
. …………………………7分②当
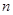 为奇数时,要使不等式
为奇数时,要使不等式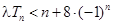 恒成立,即需不等式
恒成立,即需不等式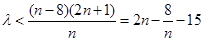 恒成立. ……………………………8分
恒成立. ……………………………8分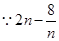 是随
是随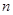 的增大而增大,
的增大而增大, 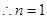 时
时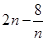 取得最小值
取得最小值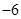 .
. 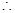 此时
此时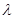 需满足
需满足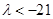 . …………………………9分
. …………………………9分综合①、②可得
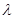 的取值范围是
的取值范围是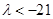 . …………………………10分
. …………………………10分(3)
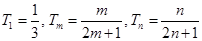 ,
, 若
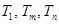 成等比数列,则
成等比数列,则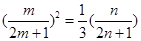 ,即
,即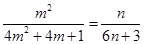 .11分
.11分(法一)由
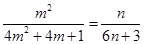 , 可得
, 可得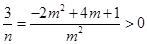 ,
,即
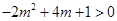 , ……………………12分
, ……………………12分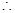
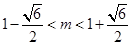 . ……………………13分
. ……………………13分又
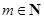 ,且
,且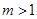 ,所以
,所以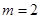 ,此时
,此时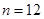 .
.因此,当且仅当
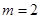 ,
, 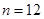 时,数列
时,数列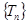 中的
中的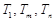 成等比数列.…………14分
成等比数列.…………14分(法二)因为
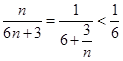 ,故
,故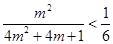 ,即
,即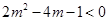 ,
,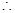
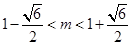 ,(以下同上).…………………13分
,(以下同上).…………………13分
练习册系列答案
相关题目

 _______________。
_______________。 ,把数列
,把数列 的各项排成如图所示的三角形状,记
的各项排成如图所示的三角形状,记 表示第i行中第j个数,则结论
表示第i行中第j个数,则结论
 ;
; ;
; ;
; .
. 满足
满足 ,
, 
 ;
;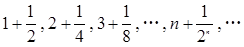 的前n项和是 .
的前n项和是 . 的通项公式
的通项公式 ,其前
,其前 项和为
项和为 ,则
,则 等于
等于 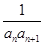 ,则数列{bn}的前
,则数列{bn}的前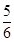


 中,
中, ,若
,若 ,则
,则 ( )
( )



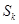 (k=1,2,3,…,n),定义
(k=1,2,3,…,n),定义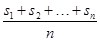 为该项数列的“凯森和”,如果项系数为99项的数列a1,a2,a3,…,a99的“凯森和”为1 000,那么项数为100的数列100,a1,a2,a3,…,a99的“凯森和”为( )
为该项数列的“凯森和”,如果项系数为99项的数列a1,a2,a3,…,a99的“凯森和”为1 000,那么项数为100的数列100,a1,a2,a3,…,a99的“凯森和”为( )