Question

16．直线l：y-1=k（x+2）与线段BC相交，设B（-1，0）、C（1，0），则直线l的斜率k的取值范围是[-1，-$\frac{1}{3}$]．

Answer 1

分析 由题意画出图形，求出定点与线段两端点连线的斜率，数形结合得答案．

解答 解：∵直线l：y-1=k（x+2）过定点P（-2，1），
如图，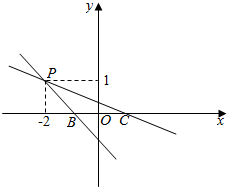

∵${k}_{PB}=\frac{1-0}{-2-（-1）}=-1$，${k}_{PC}=\frac{1-0}{-2-1}=-\frac{1}{3}$，
∴直线l的斜率k的取值范围是[-1，-$\frac{1}{3}$]．
故答案为：[-1，-$\frac{1}{3}$]．

点评 本题考查由直线和线段相交求直线斜率的范围，考查了数形结合的解题思想方法，是基础题．