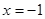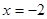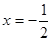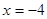题目内容
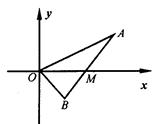
(本小题满分12分)已知抛物线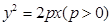 的焦点为F,过点F作直线
的焦点为F,过点F作直线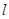 与抛物线交于A,B两点,抛物线的准线与
与抛物线交于A,B两点,抛物线的准线与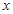 轴交于点C。
轴交于点C。
(1)证明: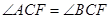 ;
;
(2)求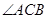 的最大值,并求
的最大值,并求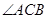 取得最大值时线段AB的长。
取得最大值时线段AB的长。
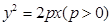 的焦点为F,过点F作直线
的焦点为F,过点F作直线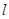 与抛物线交于A,B两点,抛物线的准线与
与抛物线交于A,B两点,抛物线的准线与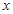 轴交于点C。
轴交于点C。(1)证明:
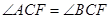 ;
;(2)求
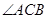 的最大值,并求
的最大值,并求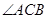 取得最大值时线段AB的长。
取得最大值时线段AB的长。解:
(Ⅰ)由题设知,F(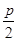 ,0),C(-
,0),C(-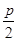 ,0),
,0),
设A(x1,y1),B(x2,y2),直线l方程为x=my+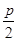 ,
,
代入抛物线方程y2=2px,得y2-2pmy-p2=0.
y1+y2=2pm,y1y2=-p2. …4分
不妨设y1>0,y2<0,则 ∴tan∠ACF=tan∠BCF,所以∠ACF=∠BCF. …8分
∴tan∠ACF=tan∠BCF,所以∠ACF=∠BCF. …8分 此时∠ACF取最大值
此时∠ACF取最大值 ,∠ACB=2∠ACF取最大值
,∠ACB=2∠ACF取最大值 ,
,
并且A(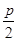 ,p),B(
,p),B(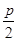 ,-p),|AB|=2p. …12分
,-p),|AB|=2p. …12分
(Ⅰ)由题设知,F(
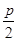 ,0),C(-
,0),C(-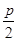 ,0),
,0),设A(x1,y1),B(x2,y2),直线l方程为x=my+
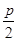 ,
,代入抛物线方程y2=2px,得y2-2pmy-p2=0.
y1+y2=2pm,y1y2=-p2. …4分
不妨设y1>0,y2<0,则
 ∴tan∠ACF=tan∠BCF,所以∠ACF=∠BCF. …8分
∴tan∠ACF=tan∠BCF,所以∠ACF=∠BCF. …8分 此时∠ACF取最大值
此时∠ACF取最大值 ,∠ACB=2∠ACF取最大值
,∠ACB=2∠ACF取最大值 ,
,并且A(
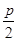 ,p),B(
,p),B(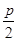 ,-p),|AB|=2p. …12分
,-p),|AB|=2p. …12分本题以直线和抛物线的位置关系为背景考查角的证明以及最值问题,考查学生的计算能力和转化能力,第一问可通过直线和方程联立,借助韦达定理和计算角的正切值进行证明;第二问借助第一问的结论,借助均值不等式进行求解最值.

练习册系列答案
相关题目
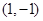 为中点的抛物线
为中点的抛物线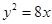 的弦所在直线方程为: .
的弦所在直线方程为: .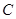 过点
过点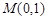 且与直线
且与直线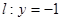 相切,设圆心
相切,设圆心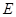 ,
,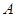 、
、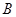 为曲线
为曲线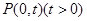 ,且满足
,且满足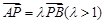 .
.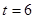 ,直线
,直线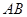 的斜率为
的斜率为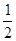 ,过
,过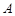 、
、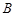 两点的圆
两点的圆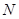 与抛物线在点
与抛物线在点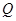 ,若点
,若点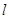 上,求证:
上,求证: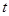 与
与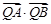 均为定值.
均为定值.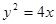 的焦点为F,点P(2,0),O为坐标原点,过P的直线
的焦点为F,点P(2,0),O为坐标原点,过P的直线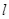 与抛物线C相交于A,B两点,若向量
与抛物线C相交于A,B两点,若向量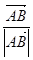 在向量
在向量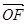 上的投影为n,且
上的投影为n,且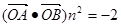 ,求直线
,求直线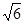 m
m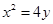 上与焦点的距离等于
上与焦点的距离等于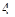 的点的纵坐标是 ( )
的点的纵坐标是 ( )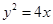 的焦点坐标为( ▲ )
的焦点坐标为( ▲ ) 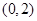
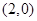
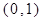
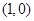

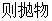
 ( )
( )