题目内容
16.已知f(x)=x(1+alnx) (a∈R)(1)若f(x)在[1,+∞)上是单调递减函数,求a的取值范围;
(2)设a=1,若k∈Z,且k(x-2)<f(x)对任意x>2恒成立,求k的最大值.
分析 (1)先求导,根据导数函数的单调性得到a≤-$\frac{1}{1+lnx}$,构造函数,求出函数的最值即可.
(2)f(x)=x(1+lnx),所以k(x-2)<f(x)对任意x>2恒成立,即k<$\frac{x+xlnx}{x-2}$对任意x>2恒成立,求出右边函数的最小值,即可求k的最大值.
解答 解:(1)∵f(x)=x(1+alnx),定义域为(0,+∞)
∴f′(x)=1+a+alnx,
∵f(x)在[1,+∞)上是单调递减函数
∴f′(x)≤0在[1,+∞)上恒成立
1+a+alnx≤0?1+a(1+lnx)≤0,
∴a≤-$\frac{1}{1+lnx}$,
令g(x)=-$\frac{1}{1+lnx}$,
∵x≥1,
∴1+lnx≥1,0<$\frac{1}{1+lnx}$≤1,
∴g(x)min=-1
于是a≤-1,即a的取值范围是(-∞,-1];
(2)a=1时,f(x)=x(1+lnx)
∵x>2,
∴k(x-2)<f(x)可化为k<$\frac{f(x)}{x-2}$=$\frac{x+xlnx}{x-2}$;
令F(x)=$\frac{x+xlnx}{x-2}$;
则F′(x)=$\frac{x-4-2lnx}{(x-2)^{2}}$;
令h(x)=x-2lnx-4,则h′(x)=1-$\frac{2}{x}$>0,
故h′(x)在(2,+∞)上是增函数,
且h′(8)=8-2ln8-4=2(2-ln8)<0,h′(9)=9-2ln9-4=5-2ln9>0;
故存在x0∈(8,9),使h′(x0)=0,即2lnx0=x0-4;
故F(x)=在(2,x0)上是减函数,在(x0,+∞)上是增函数;
故Fmin(x)=F(x0)=$\frac{{x}_{0}+{x}_{0}ln{x}_{0}}{{x}_{0}-2}$=$\frac{{x}_{0}}{2}$;
故k<$\frac{{x}_{0}}{2}$;
∴$\frac{{x}_{0}}{2}$∈(4,$\frac{9}{2}$),
由于k∈Z,
故k的最大值是4.
点评 本题考查导数知识的运用,函数的单调性,恒成立问题,函数的最值,构造函数的关键,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )
正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )| A. | 20152 | B. | 20162 | C. | 2015+2016 | D. | 2015×2016 |
| A. | -3 | B. | 3 | C. | -1 | D. | 5 |
| A. | 重心 | B. | 外心 | C. | 内心 | D. | 垂心 |
| A. | 等腰直角三角形 | B. | 等腰或直角三角形 | ||
| C. | 等腰三角形 | D. | 直角三角形 |
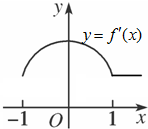 已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象可能是( )
已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象可能是( )