题目内容
8.设椭圆的对称中心为坐标原点,其中一个顶点为A(0,2),右焦点F(2$\sqrt{2}$,0).(1)求椭圆的方程;
(2)是否存在经过点(0,-3)的直线l,使直线l与椭圆相交于不同的两点M,N满足关于直线y=-$\frac{{\sqrt{6}}}{2}$x+2对称?若存在,求出直线l的方程;若不存在,请说明理由.
分析 (1)由题意设出椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(\;a>b>0\;)$,并由题意得到b,c的值,结合隐含条件求得a,则椭圆方程可求;
(2)假设存在直线l满足题目要求,可设直线l的方程为y=kx-3(k≠0),设出M、N的坐标,由MN与直线$y=-\frac{{\sqrt{6}}}{2}x+2$垂直求得直线l的斜率,得到直线l的方程,
将M、N的坐标代入椭圆方程后利用点差法得到$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=-3•\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$,代入斜率后得到关于M,N中点的一个方程,再由M、N的中点在l上得另一方程,联立求得M、N的中点坐标,验证所求中点坐标在直线y=-$\frac{{\sqrt{6}}}{2}$x+2上说明假设成立.
解答 解:(1)依题意,设椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(\;a>b>0\;)$,$c=2\sqrt{2}$,b=2,
∴a2=b2+c2=12,从而可得椭圆方程为$\frac{x^2}{12}+\frac{y^2}{4}=1$;
(2)假设存在直线l满足题目要求,可设直线l的方程为y=kx-3(k≠0),
设M(x1,y1),N(x2,y2),
∵MN与直线$y=-\frac{{\sqrt{6}}}{2}x+2$垂直,则$-\frac{\sqrt{6}}{2}k=-1$,k=$\frac{\sqrt{6}}{3}$.
∴直线l方程为:$y=\frac{{\sqrt{6}}}{3}x-3$,
将M(x1,y1),N(x2,y2)代入椭圆方程$\frac{x^2}{12}+\frac{y^2}{4}=1$,并作差,整理得:$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=-3•\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$(*),
$k=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{{\sqrt{6}}}{3}$,
设MN中点P(xp,yp),则${x_p}=\frac{{{x_1}+{x_2}}}{2},{y_p}=\frac{{{y_1}+{y_2}}}{2}$,
代入*得:$\frac{{\sqrt{6}}}{3}=-3\frac{x_p}{y_p}$,即${x_p}=-\sqrt{6}{y_p}$,
∵P(xp,yp)在MN上,∴${y_p}=\frac{{\sqrt{6}}}{3}{x_p}-3$,
联立$\left\{{\begin{array}{l}{{x_p}=-\sqrt{6}{y_p}}\\{{y_p}=\frac{{\sqrt{6}}}{3}{x_p}-3}\end{array}}\right.$,解得$\left\{{\begin{array}{l}{{x_p}=\sqrt{6}}\\{{y_p}=-1}\end{array}}\right.$.
经检验$P({\sqrt{6},-1})$满足直线方程$y=-\frac{{\sqrt{6}}}{2}x+2$,MN与直线$y=-\frac{{\sqrt{6}}}{2}x+2$垂直,且线段MN中点P在直线上,
∴存在满足条件的直线,直线l方程为$y=\frac{{\sqrt{6}}}{3}x-3$.
点评 本题考查椭圆方程的求法,主要考查了直线与椭圆的位置关系的应用,训练了“点差法”在解决中点弦问题中的应用,属中高档题.

 名校课堂系列答案
名校课堂系列答案| A. | -sin4x | B. | cos4x | C. | sinx | D. | -cosx |
| A. | a≥1 | B. | a≤1 | C. | a≥-1 | D. | a≤-3 |
| A. | [-6,2] | B. | [-6,0)∪( 0,2] | C. | [-2,0)∪( 0,6] | D. | (0,2] |
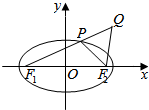 已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.
已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.