题目内容
3.给出下列四个命题:①圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9相交;
②总体的概率密度函数f(x)=$\frac{1}{\sqrt{2π}}$e${\;}^{-\frac{(x-3)^{2}}{2}}$,x∈R的图象关于直线x=3对称;f(x)的最大值为$\frac{1}{\sqrt{2π}}$.
③已知Sn是等差数列{an}的前n项和,若S7>S5,则S9>S3;
④若函数y=f(x-$\frac{3}{2}$)为R上的奇函数,则函数y=f(x)的图象一定关于点F($\frac{3}{2}$,0)成中心对称.
其中所有正确命题的序号为①②③.
分析 求出圆心距,并判断与半径和与半径差的关系,可判断①;分析函数函数f(x)=$\frac{1}{\sqrt{2π}}$e${\;}^{-\frac{(x-3)^{2}}{2}}$,x∈R的图象和性质,可判断②;根据等差数列的性质可说明③正确;直接由函数图象的平移说明④错误.
解答 解:圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的半径分别为2,3,
故半径和为5,半径差为1,
圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的圆心距d=$\sqrt{(2+2)^{2}+1}$=$\sqrt{17}$∈[1,5],
故圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9相交,故①正确;
函数f(x)=$\frac{1}{\sqrt{2π}}$e${\;}^{-\frac{(x-3)^{2}}{2}}$,f(6-x)=$\frac{1}{\sqrt{2π}}{e}^{{\;}^{-\frac{{(6-x-3)}^{2}}{2}}}$=$\frac{1}{\sqrt{2π}}{e}^{{\;}^{-\frac{{(3-x)}^{2}}{2}}}$=$\frac{1}{\sqrt{2π}}{e}^{{\;}^{-\frac{{(x-3)}^{2}}{2}}}$=f(x),故函数f(x)的图象关于直线x=3对称;
由${\;}^{-\frac{{(x-3)}^{2}}{2}}$的最大值为0,故x=3时,f(x)的最大值为$\frac{1}{\sqrt{2π}}$.故②正确;
等差数列{an}若S7>S5,则2a1+11d>0,则S9-S3=6a1+33d>0,即S9>S3,命题③正确;
对于④,函数y=f(x-$\frac{3}{2}$)为R上的奇函数,则其图象关于(0,0)中心对称,
而函数y=f(x)的图象是把y=f(x-$\frac{3}{2}$)的图象向左平移$\frac{3}{2}$个单位得到的,
∴函数y=f(x)的图象一定关于点F(-$\frac{3}{2}$,0)成中心对称.命题④错误.
故正确命题的序号为:①②③
故答案为:①②③.
点评 本题考查了命题的真假判断与应用,考查了圆的位置关系,函数图象和性质,等差数列,考查了函数图象的平移,是中档题.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案| A. | c>b>a | B. | b>c>a | C. | a>c>b | D. | a>b>c |
 如图1,在Rt△ACB中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置.
如图1,在Rt△ACB中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置.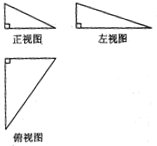 一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个几何体的外接球的表面积为21π.
一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是1,2,4,则这个几何体的外接球的表面积为21π. A,B两名学生在5次英语口语测试中的成绩统计如茎叶图所示(十位作为茎).
A,B两名学生在5次英语口语测试中的成绩统计如茎叶图所示(十位作为茎).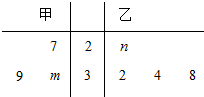 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则二项式${(\frac{x}{m}+\frac{n}{x})^4}$展开式中的常数项为$\frac{128}{3}$.
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则二项式${(\frac{x}{m}+\frac{n}{x})^4}$展开式中的常数项为$\frac{128}{3}$.