题目内容
【题目】如图,正方体![]() 的棱长为2,P是BC的中点,点Q是棱
的棱长为2,P是BC的中点,点Q是棱![]() 上的动点.
上的动点.
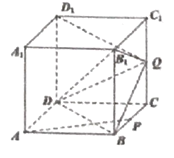
(1)点Q在何位置时,直线![]() ,DC,AP交于一点,并说明理由;
,DC,AP交于一点,并说明理由;
(2)求三棱锥![]() 的体积;
的体积;
(3)棱![]() 上是否存在动点Q,使得
上是否存在动点Q,使得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在指出点Q在棱
,若存在指出点Q在棱![]() 上的位置,若不存在,请说明理由.
上的位置,若不存在,请说明理由.
【答案】(1)当Q是![]() 中点时,直线
中点时,直线![]() ,DC,AP交于一点,理由详见解析;(2)
,DC,AP交于一点,理由详见解析;(2)![]() ;(3)存在点Q,且点Q为
;(3)存在点Q,且点Q为![]() 的中点.
的中点.
【解析】
(1)画出辅助线延长AP交DC于M,连结![]() 交
交![]() 于点Q,利用相似三角形证明即可.
于点Q,利用相似三角形证明即可.
(2)换顶点求解三棱锥![]() 的体积即可.
的体积即可.
(3)以D为原点建立合适的空间直角坐标系,设![]() ,再利用线面夹角的向量解法求出
,再利用线面夹角的向量解法求出![]() 即可.
即可.
解:(1)当Q是![]() 中点时,直线
中点时,直线![]() ,DC,AP交于一点.
,DC,AP交于一点.
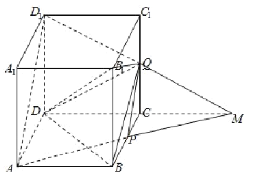
理由如下:延长AP交DC于M,连结![]() 交
交![]() 于点Q,
于点Q,
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,∴
,∴![]() .
.
∴Q是![]() 中点.
中点.
(2)V棱锥![]() 棱锥
棱锥![]() .
.
(3)以D为原点,DA,DC,![]() 所在直线分别为x轴,y轴,z轴,建系
所在直线分别为x轴,y轴,z轴,建系
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
设面![]() 的法向量为
的法向量为![]() ,则
,则
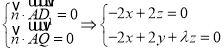
取![]() ,
,![]() ,
,![]() 即
即![]()
设![]() 与面
与面![]() 所成角为
所成角为![]()
则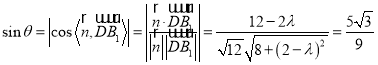
化简得![]()
解得![]() 或
或![]() (舍去)
(舍去)
所以存在点Q,且点Q为![]() 的中点
的中点

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目