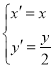题目内容
【题目】已知椭圆C：
的左右焦点分别为F1、F2，过F1的直线交椭圆C与A、B两点，△AF2B的周长为
，且椭圆C经过点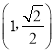
．
（1）求椭圆C的方程；
（2）当AB的中点坐标为
时，求△AF2B的面积．
【答案】（1）
y2＝1（2）
【解析】
（1）根据椭圆的定义求出a
，再由椭圆上的点满足椭圆方程求出
即可.
（2）根据已知设出直线方程，将直线与椭圆联立，利用中点弦公式求出直线方程，
再由弦长公式以及点到直线的距离即可求解.
（1）∵△AF2B的周长为4
，故4a＝4，即a，
又椭圆经过点（1，
），∴
1，即b＝1，
∴椭圆方程为y2＝1．
（2）由椭圆方程可知F1（﹣1，0），F2（1，0）．
∵AB的中点（
，
）在第二象限，显然直线AB有斜率且斜率大于0，
设直线AB的方程为y＝k（x+1）（k＞0），
代入椭圆方程可得：（
k2）x2+2k2x+k2﹣1＝0，
设A（x1，y1），B（x2，y2），即
，
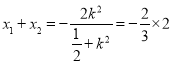解得：k＝1，于是x1x2＝0，
∴|AB|
．
又直线AB的方程为：y＝x+1，F2（1，0），
∴F2到直线AB的距离d
，
∴△ABF2的面积为
．
练习册系列答案
相关题目
