题目内容
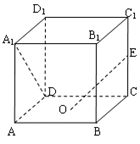
如图,在棱长为2的正方体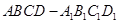 中,
中,
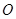 为底面的中心,
为底面的中心,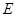 是
是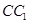 的中点,那么异面直线
的中点,那么异面直线
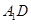 与
与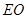 所成角的余弦值为
所成角的余弦值为
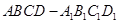 中,
中,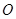 为底面的中心,
为底面的中心,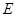 是
是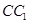 的中点,那么异面直线
的中点,那么异面直线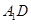 与
与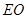 所成角的余弦值为
所成角的余弦值为 A. | B. | C.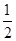 | D. |

D
本题可以建立空间坐标系,求出两异面直线的方向向量,利用数量积公式求出两向量夹角余弦的绝对值,即所求的异面直线A1D与EO所成角的余弦值
解答:解:如图以DA所在直线为X轴,
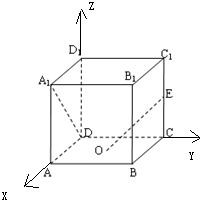
以DC所在直线为Y轴,以DD1所在直线为Z轴建立如图的坐标系,由题设条件棱长为2,O为底面的中心,E是CC1的中点,故有A1(2,0,2),D(0,0,0),O(1,1,0),E(0,2,1)
故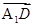 =(-2,0,-2),
=(-2,0,-2),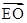 =(-1,1,1),
=(-1,1,1),
cos<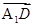 ,
,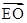 >=
>=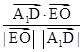 =
=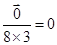
故选D
解答:解:如图以DA所在直线为X轴,

以DC所在直线为Y轴,以DD1所在直线为Z轴建立如图的坐标系,由题设条件棱长为2,O为底面的中心,E是CC1的中点,故有A1(2,0,2),D(0,0,0),O(1,1,0),E(0,2,1)
故
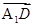 =(-2,0,-2),
=(-2,0,-2),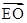 =(-1,1,1),
=(-1,1,1),cos<
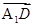 ,
,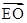 >=
>=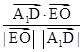 =
=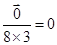
故选D

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
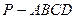 中,底面
中,底面 是矩形.已知
是矩形.已知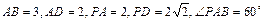 .
.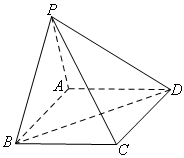
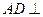 平面
平面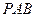 ;
;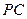 与
与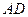 所成的角的大小;
所成的角的大小;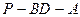 的大小.
的大小.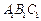 中,AB=1,
中,AB=1,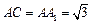 ,
,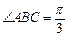 .
.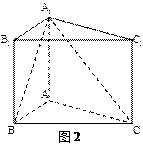
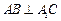 ;
;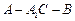 的正弦值.
的正弦值.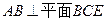 ,
,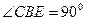 . 点
. 点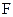 是
是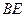 的中点. 求证:
的中点. 求证: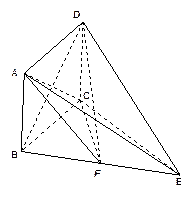
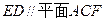
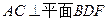
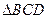 与
与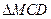 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面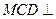 平面
平面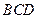 ,
,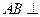 平面BCD,
平面BCD,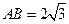 .求点A到平面MBC的距离。
.求点A到平面MBC的距离。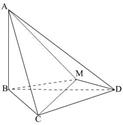
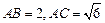 .
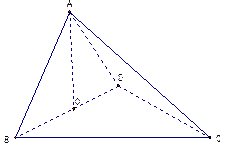
.
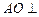 平面BCD;
平面BCD; 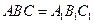 中,AB⊥BC,D为AC的中点,
中,AB⊥BC,D为AC的中点,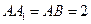 。
。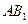 ∥平面
∥平面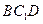 ;
;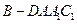 的体积为2,求二面角
的体积为2,求二面角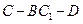 的正切值。
的正切值。
 的底面ABCD是正方形,侧棱
的底面ABCD是正方形,侧棱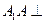 底面ABCD,E、F分别是C1D1,C1B1的中点,G为CC1上任一点
底面ABCD,E、F分别是C1D1,C1B1的中点,G为CC1上任一点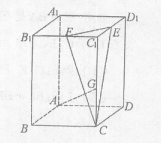
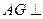 平面CEF,并说明理由;
平面CEF,并说明理由;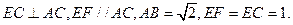

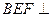 平
平 面DEF;
面DEF; 角A—BF—E的大小。
角A—BF—E的大小。