题目内容
(本小题满分12分)
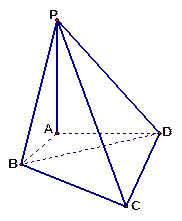
如图,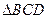 与
与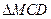 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面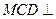 平面
平面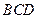 ,
,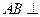 平面BCD,
平面BCD,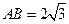 .求点A到平面MBC的距离。
.求点A到平面MBC的距离。
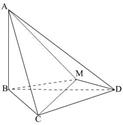
如图,
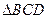 与
与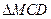 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面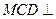 平面
平面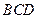 ,
,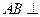 平面BCD,
平面BCD,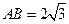 .求点A到平面MBC的距离。
.求点A到平面MBC的距离。
解法一: (Ⅰ)如图,以A为坐标原点,AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系.
∵AP=AB=2,BC=AD= ,四边形ABCD是矩形.
,四边形ABCD是矩形.
∴A,B,C,D,P的坐标为A(0,0,0),B(2,0,0),C(2, ,0),D(0,
,0),D(0, ,0),P(0,0,2),
,0),P(0,0,2),
又E,F分别是AD ,PC的中点,
,PC的中点,
∴E(0,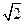 ,0),F(1,
,0),F(1,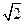 ,1).
,1).
∴ =(2,
=(2, ,-2)
,-2) =(-1,
=(-1,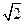 ,1)
,1)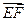 =(1,0,
=(1,0, 1),
1),
∴ ·
· =-2+4-2=0,
=-2+4-2=0, ·
·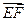 =2+0-2=0,
=2+0-2=0,
∴ ⊥
⊥ ,
, ⊥
⊥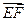 ,
,
∴PC⊥BF,PC⊥EF,BF ∩ EF=F,
∴PC⊥平面B EF,
EF,
(II)由(I)知平面BEF的法向量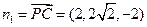 ,
,
平面BAP 的法向量 ,
,
∴ . 设平面BEF与平面BAP的夹角为 θ ,
. 设平面BEF与平面BAP的夹角为 θ ,
则 ,
,
∴ θ=45°, ∴ 平面BEF与平面BAP的夹角为45°.
解法二 (I)连接PE,EC在 和
和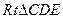 中.
中.
PA="AB=CD," AE=DE,
∴ PE=" CE," 即 △PEC 是等腰三角形,
又F是PC 的中点,∴EF⊥PC,
又 ,F是PC 的中点,
,F是PC 的中点,
∴ BF⊥PC.
又 ,∴
,∴ .
.
(II)∵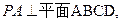 ∴
∴ ,
,
又ABCD是矩形,∴AB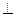 BC
BC
∴BC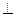 平面BAP,B
平面BAP,B C
C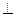 PB,
PB,
又由(Ⅰ)知PC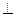 平面BEF,
平面BEF,
∴ 直线PC与BC的夹角即为平面BEF与平面BAP的夹角,
在 中,
中, ∴
∴
所以平面BEF与平面BAP的夹角为45°.
∵AP=AB=2,BC=AD=
 ,四边形ABCD是矩形.
,四边形ABCD是矩形.∴A,B,C,D,P的坐标为A(0,0,0),B(2,0,0),C(2,
 ,0),D(0,
,0),D(0, ,0),P(0,0,2),
,0),P(0,0,2),又E,F分别是AD
 ,PC的中点,
,PC的中点,∴E(0,
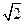 ,0),F(1,
,0),F(1,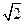 ,1).
,1).∴
 =(2,
=(2, ,-2)
,-2) =(-1,
=(-1,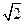 ,1)
,1)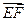 =(1,0,
=(1,0, 1),
1),∴
 ·
· =-2+4-2=0,
=-2+4-2=0, ·
·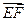 =2+0-2=0,
=2+0-2=0,∴
 ⊥
⊥ ,
, ⊥
⊥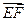 ,
,∴PC⊥BF,PC⊥EF,BF ∩ EF=F,
∴PC⊥平面B
 EF,
EF,(II)由(I)知平面BEF的法向量
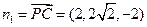 ,
,平面BAP 的法向量
 ,
,∴
 . 设平面BEF与平面BAP的夹角为 θ ,
. 设平面BEF与平面BAP的夹角为 θ ,则
 ,
,∴ θ=45°, ∴ 平面BEF与平面BAP的夹角为45°.
解法二 (I)连接PE,EC在
 和
和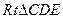 中.
中. PA="AB=CD," AE=DE,
∴ PE=" CE," 即 △PEC 是等腰三角形,
又F是PC 的中点,∴EF⊥PC,
又
 ,F是PC 的中点,
,F是PC 的中点,∴ BF⊥PC.
又
 ,∴
,∴ .
.(II)∵
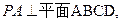 ∴
∴ ,
,又ABCD是矩形,∴AB
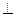 BC
BC∴BC
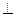 平面BAP,B
平面BAP,B C
C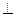 PB,
PB,又由(Ⅰ)知PC
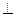 平面BEF,
平面BEF,∴ 直线PC与BC的夹角即为平面BEF与平面BAP的夹角,
在
 中,
中, ∴
∴
所以平面BEF与平面BAP的夹角为45°.
略

练习册系列答案
相关题目
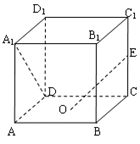
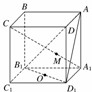
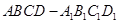 中,
中,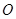 为底面的中心,
为底面的中心,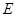 是
是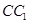 的中点,那么异面直线
的中点,那么异面直线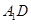 与
与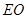 所成角的余弦值为
所成角的余弦值为 

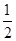

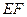 ⊥平面
⊥平面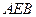 ,
,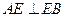 ,
,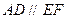 ,
,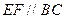 ,
,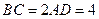 ,
,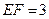 ,
,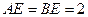 ,
,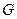 是
是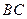 的
的 中点.
中点.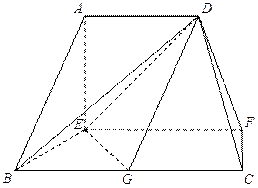
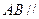 平面
平面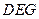 ;
;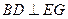 ;
;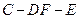 的余弦值.
的余弦值. 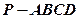 ,
,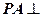 平面
平面 ,
,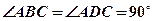 ,
,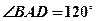 ,
, ,
,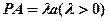 .
.
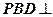 平面
平面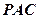 ;
;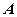 到平面
到平面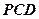 的距离为
的距离为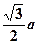 时,求二面角
时,求二面角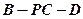 的余弦值;
的余弦值;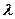 为何值时,点
为何值时,点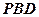 内的射影
内的射影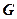 恰好是
恰好是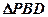 的重心.
的重心.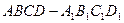 ,
,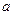 ,底面是正方形,且
,底面是正方形,且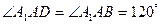 ,
,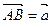 ,
,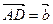 ,
,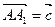 ,
,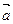 、
、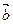 、
、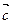 表示
表示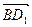 及求
及求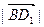 ;
;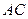 与
与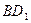 所成的角的余弦值。
所成的角的余弦值。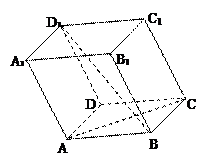
 10分)
10分)
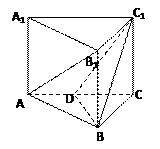

 中,DA = DC
中,DA = DC =2,
=2,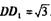 ’E是
’E是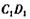 的中点,F是C/:的中点.
的中点,F是C/:的中点.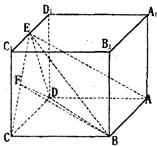
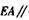 平面BDF
平面BDF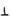 平面
平面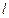
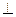 平面
平面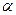 ,平面
,平面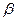 //直线
//直线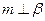 ,则
,则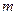 //
//