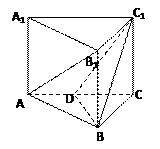题目内容
((本小题满分12分)
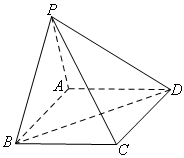
如图,在四棱锥 中,底面
中,底面 是矩形.已知
是矩形.已知
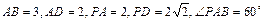 .
.
(1)证明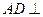 平面
平面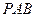 ;
;
(2)求异面直线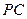 与
与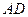 所成的角的大小;
所成的角的大小;
(3)求二面角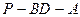 的大小.
的大小.
如图,在四棱锥
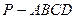 中,底面
中,底面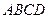 是矩形.已知
是矩形.已知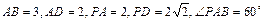 .
.
(1)证明
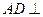 平面
平面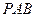 ;
;(2)求异面直线
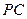 与
与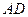 所成的角的大小;
所成的角的大小;(3)求二面角
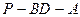 的大小.
的大小.解:(1)证明:在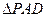 中,由题设
中,由题设 可得
可得
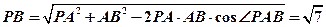
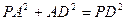 于是
于是 . …… 2分
. …… 2分
在矩形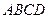 中,
中,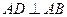 .又
.又 ,
,
所以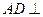 平面
平面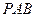 .
.  ………… 4分
………… 4分
(2)解:由题设,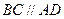 ,所以
,所以 (或其补角)是异面直线
(或其补角)是异面直线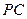 与
与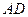 所成的角. … 5分
所成的角. … 5分
在 中,由余弦定理得
中,由余弦定理得
……… 6分
由(1)知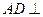 平面
平面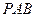 ,
,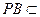 平面
平面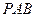 ,
,
所以 ,因而
,因而 , ……… 7分
, ……… 7分
于是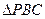 是直角三角形,故
是直角三角形,故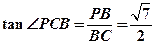 .
.
所以异面直线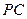 与
与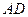 所
所 成的角的大小为
成的角的大小为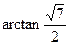 .……… 8分
.……… 8分
(3)解:过点P做 于H,过点H做
于H,过点H做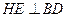 于E,连结PE
于E,连结PE
因为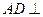 平面
平面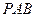 ,
,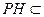 平面
平面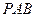 ,所以
,所以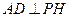 .又
.又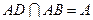 ,
,
因而 平面
平面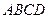 ,故HE为PE在平面ABCD内的射影.由三垂线定理可知,
,故HE为PE在平面ABCD内的射影.由三垂线定理可知,
 ,从而
,从而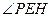 是二面角
是二面角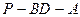 的平面角。……… 9分
的平面角。……… 9分
由题设可得,
 ……… 10分
……… 10分
于是在 中,
中,
所以二面角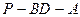 的大小为
的大小为 . ……… 12分
. ……… 12分
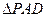 中,由题设
中,由题设 可得
可得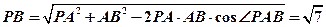
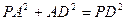 于是
于是 . …… 2分
. …… 2分在矩形
 中,
中,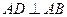 .又
.又 ,
,所以
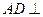 平面
平面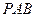 .
.  ………… 4分
………… 4分(2)解:由题设,
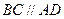 ,所以
,所以 (或其补角)是异面直线
(或其补角)是异面直线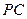 与
与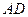 所成的角. … 5分
所成的角. … 5分在
 中,由余弦定理得
中,由余弦定理得……… 6分
由(1)知
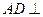 平面
平面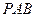 ,
,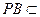 平面
平面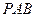 ,
,所以
 ,因而
,因而 , ……… 7分
, ……… 7分于是
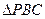 是直角三角形,故
是直角三角形,故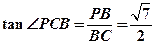 .
.所以异面直线
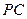 与
与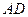 所
所 成的角的大小为
成的角的大小为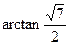 .……… 8分
.……… 8分(3)解:过点P做
 于H,过点H做
于H,过点H做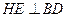 于E,连结PE
于E,连结PE因为
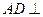 平面
平面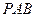 ,
,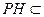 平面
平面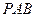 ,所以
,所以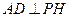 .又
.又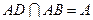 ,
,因而
 平面
平面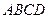 ,故HE为PE在平面ABCD内的射影.由三垂线定理可知,
,故HE为PE在平面ABCD内的射影.由三垂线定理可知, ,从而
,从而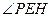 是二面角
是二面角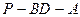 的平面角。……… 9分
的平面角。……… 9分由题设可得,
 ……… 10分
……… 10分于是在
 中,
中,
所以二面角
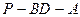 的大小为
的大小为 . ……… 12分
. ……… 12分略

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 的正方体
的正方体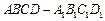 中,
中,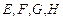 分别是棱
分别是棱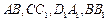 的中点.
的中点.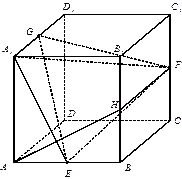
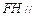 平面
平面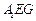 ;
;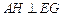 ;
;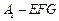 的体积.
的体积.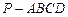 的底面
的底面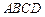 为菱形,
为菱形,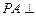 平面
平面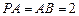 ,
,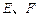 分别为
分别为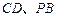 的中点,
的中点,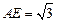 .
.
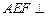 平面
平面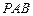 .
.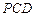 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.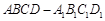 中,棱长都相等;条件乙:直四棱柱
中,棱长都相等;条件乙:直四棱柱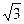 。AD=
。AD=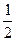 。
。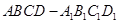 中,
中,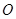 为底面的中心,
为底面的中心,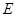 是
是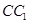 的中点,那么异面直线
的中点,那么异面直线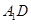 与
与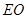 所成角的余弦值为
所成角的余弦值为 

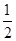

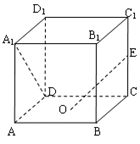
 过点
过点 ,且
,且 是它的一个法向量,则
是它的一个法向量,则 (本小题满分12分)
(本小题满分12分)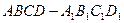 的下底面
的下底面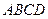 是边长为
是边长为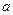 的正方形,
的正方形,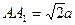 ,且点
,且点 在下底面
在下底面 点.
点.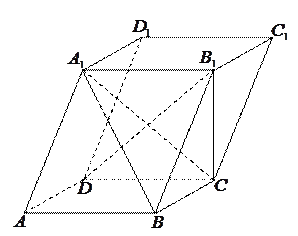
 面
面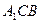 ;
;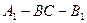 的大小.
的大小. 10分)
10分)