题目内容
(本小题满分13分已知 相的中心在原点,焦点在x轴上,离心率为
相的中心在原点,焦点在x轴上,离心率为 ,点F1、F2分别是椭圆的左、右焦点,
,点F1、F2分别是椭圆的左、右焦点,
直线x=2是椭圆的准线方程,直线 与椭圆C
与椭圆C
交地不同的两点A、B。 (I)求椭圆C的方程;(II)若在椭圆C上存在点Q,满足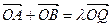 (O为坐标原点),求实数
(O为坐标原点),求实数 的取值范围。
的取值范围。
 相的中心在原点,焦点在x轴上,离心率为
相的中心在原点,焦点在x轴上,离心率为 ,点F1、F2分别是椭圆的左、右焦点,
,点F1、F2分别是椭圆的左、右焦点,直线x=2是椭圆的准线方程,直线
 与椭圆C
与椭圆C交地不同的两点A、B。 (I)求椭圆C的方程;(II)若在椭圆C上存在点Q,满足
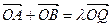 (O为坐标原点),求实数
(O为坐标原点),求实数 的取值范围。
的取值范围。(Ⅰ)  (Ⅱ)
(Ⅱ) 
 (Ⅱ)
(Ⅱ) 
(I)依题意有 解得
解得
 所求椭圆方程为
所求椭圆方程为 (5分)
(5分)
(Ⅱ)由 得
得
∵△=
 ,
,
∴由△>0,得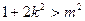 ①
①
设点A、B的坐标分别为A( ,
, ),B(
),B( ,
, )
)
则


 8分
8分
(1)当 时,点A、B关于原点对称,则
时,点A、B关于原点对称,则
(2)当 ≠0时,点A、B不关于原点对称,则
≠0时,点A、B不关于原点对称,则
由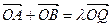 ,得
,得 即
即 ∵点Q在椭圆上,
∵点Q在椭圆上,
∴有 ,化简,得
,化简,得 ∵
∵ ≠0,
≠0,
∴有 ②11分①②两式得
②11分①②两式得 ,
,
∵m≠0,∴ ,则
,则 且
且 ≠0
≠0
综合(1)(2)两种情况,得实数 的取值范围是
的取值范围是 13分
13分
 解得
解得
 所求椭圆方程为
所求椭圆方程为 (5分)
(5分)(Ⅱ)由
 得
得
∵△=

 ,
,∴由△>0,得
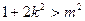 ①
①设点A、B的坐标分别为A(
 ,
, ),B(
),B( ,
, )
)则



 8分
8分(1)当
 时,点A、B关于原点对称,则
时,点A、B关于原点对称,则
(2)当
 ≠0时,点A、B不关于原点对称,则
≠0时,点A、B不关于原点对称,则
由
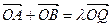 ,得
,得 即
即 ∵点Q在椭圆上,
∵点Q在椭圆上,∴有
 ,化简,得
,化简,得 ∵
∵ ≠0,
≠0,∴有
 ②11分①②两式得
②11分①②两式得 ,
,∵m≠0,∴
 ,则
,则 且
且 ≠0
≠0综合(1)(2)两种情况,得实数
 的取值范围是
的取值范围是 13分
13分
练习册系列答案
相关题目
 中,已知
中,已知 ,且当顶点
,且当顶点 位于定点
位于定点 时,
时, 有最小值为
有最小值为 .(1)建立适当的坐标系,求顶点
.(1)建立适当的坐标系,求顶点 作直线与(1)中的曲线交于
作直线与(1)中的曲线交于 、
、 两点,求
两点,求 的最小值的集合.
的最小值的集合. 左右焦点分别为
左右焦点分别为 、
、 ,点
,点 在椭圆上,若
在椭圆上,若 轴的距离为( )
轴的距离为( ) B 3 C
B 3 C  D
D 





 d,
d, ≤d≤
≤d≤ .
. ·
· =
= ,求向量
,求向量 与
与 与直线
与直线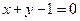 相交于两点
相交于两点 .
. ,且
,且 成等差数列时,求椭圆的方程;
成等差数列时,求椭圆的方程; 的长度
的长度 ;
;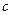 是椭圆
是椭圆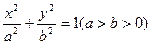 的半焦距,则
的半焦距,则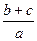 的取值范围是 ( )
的取值范围是 ( )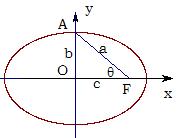
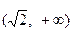 C
C 
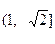
 +
+ =1与
=1与 +
+ =1(0<k<9)的关系为( )
=1(0<k<9)的关系为( ) ,
, ,则
,则 的轨迹方程是
的轨迹方程是