题目内容
【题目】已知向量 
=（ 
sin 
，1）， 
=（cos ，cos2 ）． （Ⅰ）若 =1，求cos（ 
﹣x）的值；
（Ⅱ）记f（x）= ，在△ABC中，A、B、C的对边分别为a、b、c，且满足（2a﹣c）cosB=bcosC，求函数f（A）的取值范围．
【答案】解：（Ⅰ） ∵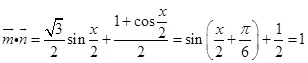 
∴ 
∵ 
（Ⅱ）∵（2a﹣c）cosB=bcosC
∴2sinAcosB=sinCcosB+sinBcosC=sin（B+C）=sinA
∵sinA＞0
∴cosB= 
∵B∈（0，π），
∴ 
∴ 
∵ 
∴ 
∵ 
∴ 
∴ 
【解析】（Ⅰ）利用向量的数量积公式列出方程求出 
，利用二倍角的余弦公式求出要求的式子的值．（Ⅱ）利用三角形中的正弦定理将等式中的边转化为角的正弦值，利用三角形的内角和为180°化简等式，求出角B，求出角A的范围，求出三角函数值的范围．
【考点精析】掌握两角和与差的余弦公式和正弦定理的定义是解答本题的根本，需要知道两角和与差的余弦公式：
；正弦定理:
．
练习册系列答案
相关题目
