题目内容
4. 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E是PC的中点.(Ⅰ)证明:PA∥平面EBD;
(Ⅱ)若直线PC与平面EBD所成角的大小为60°,求PA的长.
分析 (Ⅰ)连接AC交BD于点O,连接OE,证明EO∥PA,然后证明PA∥平面FBD.
(Ⅱ) 解法一:说明∠CEO就是直线PC与平面EDB所成角然后求解PA.
解法二:以O为坐标原点,分别以射线OA,OB,OE为x,y,z轴的正半轴,建立空间直角坐标系O-xyz,平面EBD的法向量为$\overrightarrow{m}$=(1,0,0),利用向量的数量积求解PA即可.
解答 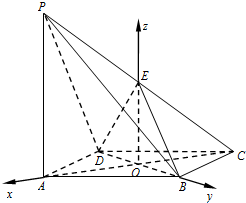
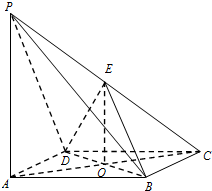 解:(Ⅰ)证明:连接AC交BD于点O,连接OE,
解:(Ⅰ)证明:连接AC交BD于点O,连接OE,
∵O、E分别是AC、PC的中点,
∴EO∥PA.…(5分)
∵PA不在平面FBD内,
∴PA∥平面FBD.…(7分)
(Ⅱ) 解法一:∵PA⊥平面ABCD,∴PA⊥AC,
又∵EO∥PA,∴EO⊥AC,又AC⊥BD,
∴AC⊥平面EBD,
∴∠CEO就是直线PC与平面EDB所成角.…(11分)
在菱形ABCD中,容易求得$OC=\frac{{\sqrt{3}}}{2}$.
又∵EO⊥OC,所以$EO=\frac{1}{2}$,故PA=1.…(15分)
解法二:因为EO∥PA,PA⊥底面ABCD,∴EO⊥底面ABCD,又AC⊥BD,以O为坐标原
点,分别以射线OA,OB,OE为x,y,z轴的正半轴,建立空间直角坐标系O-xyz,如图所示.
设PA=h,由题意可知各点坐标如下:
A$({\frac{{\sqrt{3}}}{2},0,0})$,C$({-\frac{{\sqrt{3}}}{2},0,0})$,P$({\frac{{\sqrt{3}}}{2},0,h})$,…(11分)
平面EBD的法向量为$\overrightarrow{m}$=(1,0,0),$\overrightarrow{PC}=({\sqrt{3},0,h})$,
由已知可得,$|cos<m,\overrightarrow{PC}>|=sin60°$,即$\frac{{\sqrt{3}}}{{\sqrt{3+{h^2}}}}=\frac{{\sqrt{3}}}{2}$,
∴h=1,即PA=1.…(15分)
点评 本题考查空间点线面距离的求法,直线与平面所成角,直线与平面平行的判定定理的应用,考查逻辑推理能力.


| A. | [-3,3] | B. | [-1,2] | C. | [-3,-1] | D. | [2,3] |
| A. | 3 | B. | $\sqrt{15}$ | C. | 3或5 | D. | 3或$\sqrt{15}$ |