题目内容
15.已知函数f(x)=ax3-x2+bx(a,b∈R),曲线y=f(x)在点(3,f(3))处的切线方程为y=-9.(1)求f(x)的单调递减区间;
(2)记g(x)=f′(x)-kxlnx-k(k为正整数,f′(x)为y=f(x)导函数),曲线y=g(x)上的点都在不等式y>-6x-4表示的平面区域内,求k的最大值.
分析 (1)求导数,利用曲线y=f(x)在点(3,f(3))处的切线方程为y=-9,建立方程,求出a,b,即可求f(x)的单调递减区间;
(2)曲线y=g(x)上的点都在不等式y>-6x-4表示的平面区域内,等价于x2+4x+1-kxlnx+k>0,构造函数求最值,即可得出结论.
解答 解:(1)∵f(x)=ax3-x2+bx,
∴f′(x)=3ax2-2x+b,
∵曲线y=f(x)在点(3,f(3))处的切线方程为y=-9,
∴f′(3)=0,f(3)=-9,
∴$\left\{\begin{array}{l}{27a-6+b=0}\\{27a-9+3b=-9}\end{array}\right.$,
∴a=$\frac{1}{3}$,b=-3,
∴f′(x)=(x+1)(x-3),
令f′(x)<0,可,得-1<x<3,
∴f(x)的单调递减区间是(-1,3);
(2)g(x)=x2-2x-3-kxlnx+k,
∴曲线y=g(x)上的点都在不等式y>-6x-4表示的平面区域内,等价于x2+4x+1-kxlnx+k>0,
即x+$\frac{k+1}{x}+4-klnx$>0,
记φ(x)=x+$\frac{k+1}{x}+4-klnx$,则φ′(x)=$\frac{(x+1)(x-k-1)}{{x}^{2}}$,
由φ′(x)>0得x>k+1,
∴φ(x)在(0,k+1)上单调递减,在(k+1,+∞)上单调递增,
∴φ(x)≥φ(k+1)>0,
∴k+6-kln(k+1)>0,
即1+$\frac{6}{k}$-ln(k+1)>0
记m(x)=1+$\frac{6}{x}$-ln(x+1),则m′(x)=-$\frac{6}{{x}^{2}}-\frac{1}{x+1}$<0,
∴m(x)在(0,+∞)上单调递减,
∵m(6)=2-ln7>0,m(7)=$\frac{13}{7}$-ln8<0,
∴k的最大值为6.
点评 本题考查导数知识的综合运用,考查函数的单调性与几何意义,考查函数的最值,正确构造函数是关键.

| A. | $-\frac{π}{6}$ | B. | $-\frac{π}{12}$ | C. | $\frac{π}{12}$ | D. | $\frac{π}{6}$ |
表1:男生
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
(2)从表二中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
临界值表:
| P(K2>k0) | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
 已知四棱锥S-ABCD的底面为菱形,且∠ABC=60°,AB=AC=2,SA=SB=$\sqrt{2}$
已知四棱锥S-ABCD的底面为菱形,且∠ABC=60°,AB=AC=2,SA=SB=$\sqrt{2}$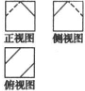 一个棱长为1的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{24}$.
一个棱长为1的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{24}$. 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E是PC的中点.