题目内容
10.三个正数a,b,c成公比大于1的等比数列,a+b+c=62,lga+lgb+lgc=3,求a、b、c.分析 由题意可得b值,可得ac的方程组,解方程组结合题意可得.
解答 解:∵lga+lgb+lgc=lgabc=3,
∴abc=b3=1000,解得b=10,
又a+b+c=62,∴a+c=52,
又ac=100,
联立解方程组可解得$\left\{\begin{array}{l}{a=2}\\{c=50}\end{array}\right.$或$\left\{\begin{array}{l}{a=50}\\{c=2}\end{array}\right.$
∵公比q>1,∴$\left\{\begin{array}{l}{a=2}\\{c=50}\end{array}\right.$,此时q=$\sqrt{\frac{50}{2}}$=5,
∴a=2,b=10,c=5
点评 本题考查等比数列的通项公式,涉及对数的运算,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.一几何体的三视图如图所示,则它的体积为( )


| A. | 2 | B. | 3 | C. | 6 | D. | 9 |
19.设S是整数集Z的非空子集,如果?a,b∈Z,都有a2-b2∈S,则称S是一个好集,已知S是一个“好集”,下面命题为假命题的是( )
| A. | 一切奇数都属于S | B. | 偶数4k-2(k∈Z)都不属于S | ||
| C. | 若x,y∈S,则xy∈S | D. | 若x,y属于S,则x+y∈S |

 如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,PD⊥面ABCD,直线PA与直线BC所成角大小为60°,求直线PB与直线AC所成角的大小.
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,PD⊥面ABCD,直线PA与直线BC所成角大小为60°,求直线PB与直线AC所成角的大小. 如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)
如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)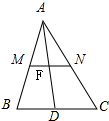 如图,已知△ABC,A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于F.
如图,已知△ABC,A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于F.