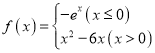题目内容
【题目】已知函数
（
，
）的图象的相邻两条对称轴之间的距离为4，且有一个零点为
.
（1）求函数
的解析式；
（2）若
，且
，求
的值；
（3）若
在
上恒成立，求实数
的取值范围.
【答案】（1）
；（2）
；（3）
【解析】
（1）根据题意，由周期和零点，求得函数对应的参数即可；
（2）由
求得
，凑角，利用正弦和角公式计算即可；
（3）将恒成立问题转化为最值问题，再求三角函数的最值即可.
（1）因为函数
图象的相邻两条对称轴之间的距离为4，
所以函数的最小正周期是8.
所以
，解得
.
所以
.
因为函数有一个零点
，
所以
，
得
（
）.
解得
（）.
由
知，
，
所以；
（2）由
，得
，
即，
由
，得
，
所以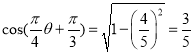
.
所以
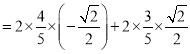
（3）由
，得
，
所以当时，
，
若
在上恒成立，
则
在上恒成立，
则
，即
，
解得
.
故
的取值范围为.
练习册系列答案
特高级教师点拨系列答案
相关题目
【题目】已知某观光海域AB段的长度为3百公里，一超级快艇在AB段航行，经过多次试验得到其每小时航行费用Q（单位：万元）与速度v（单位：百公里／小时）（0≤v≤3）的以下数据：
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
为描述该超级快艇每小时航行费用Q与速度v的关系，现有以下三种函数模型供选择：Q＝av3＋bv2＋cv，Q＝0．5v＋a，Q＝klogav＋b．
（1）试从中确定最符合实际的函数模型，并求出相应的函数解析式；
（2）该超级快艇应以多大速度航行才能使AB段的航行费用最少？并求出最少航行费用．
