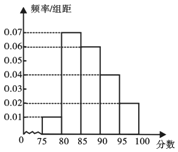
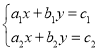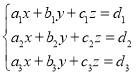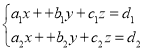题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,求证:函数
,求证:函数![]() 恰有一个负零点;(用图象法证明不给分)
恰有一个负零点;(用图象法证明不给分)
(2)若函数![]() 恰有三个零点,求实数
恰有三个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)由单调性的性质可判断出![]() 在
在![]() 上单调递减,利用零点存在定理可知存在唯一的
上单调递减,利用零点存在定理可知存在唯一的![]() 使得
使得![]() ,由此可证得结论;
,由此可证得结论;
(2)令![]() ,结合函数图象可知,若
,结合函数图象可知,若![]() 恰有三个零点,则方程
恰有三个零点,则方程![]() 必有两根
必有两根![]() ,且
,且![]() ,
,![]() 或
或![]() ,
,![]() ;当
;当![]() 时可求得
时可求得![]() ,不合题意;当
,不合题意;当![]() ,
,![]() 时,根据二次函数图象可得到不等式组,由此解得结果.
时,根据二次函数图象可得到不等式组,由此解得结果.
(1)若![]() ,则
,则![]()
![]() 时,
时,![]() 单调递减,
单调递减,![]() 单调递减
单调递减
![]() 当
当![]() 时,
时,![]() 单调递减
单调递减
又![]() ,
,![]() ,则存在唯一的
,则存在唯一的![]() 使得
使得![]()
即函数![]() 在区间
在区间![]() 恰有一个零点
恰有一个零点
(2)令![]() ,
,![]() ,要使得函数
,要使得函数![]() 恰有三个零点
恰有三个零点
![]() 图象如下图所示:
图象如下图所示:
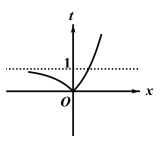
则方程![]() 必有两根
必有两根![]() ,且
,且![]() ,
,![]() 或
或![]() ,
,![]()
①若![]() ,
,![]() 时,令
时,令![]()
则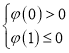 ,即
,即![]() ,解得:
,解得:![]()
②若![]() ,则
,则![]() ,即
,即![]()
![]() ,不合题意
,不合题意
综上所述:实数![]() 的取值范围为
的取值范围为![]()

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案【题目】某手机生产企业为了解消费者对某款手机的认同情况,通过销售部随机抽取50名购买该款手机的消费者,并发出问卷调查(满分50分),该问卷只有20份给予回复,这20份的评分如下:
男 | 47,36,28,48,48,44,50,46,50,37,35,49 |
女 | 38,37,50,36,38,45,29,39 |
(1)完成下面的茎叶图,并求12名男消费者评分的中位数与8名女消费者评分的众数及平均值;
男 | 女 | |
2 | ||
3 | ||
4 | ||
5 |
满意 | 不满意 | 合计 | |
男 | |||
女 | |||
合计 |
(2)若大于40分为“满意”,否则为“不满意”,完成上面的![]() 列联表,并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关;
列联表,并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关;
(3)若从回复的20名消费者中按性别用分层抽样的方法抽取5人,再从这5人中随机抽取2人作进一步调查,求至少有1名女性消费者被抽到的概率.
附:
| 0.05 | 0.025 | 0.01 |
| 3.841 | 5.024 | 6.635 |
【题目】某公司的新能源产品上市后在国内外同时销售,已知第一批产品上市销售40天内全部售完,该公司对这批产品上市后的国内外市场销售情况进行了跟踪调查,如图所示,其中图①中的折线表示的是国外市场的日销售量与上市时间的关系;图②中的抛物线表示的是国内市场的日销售量与上市时间的关系;下表表示的是产品广告费用、产品成本、产品销售价格与上市时间的关系.
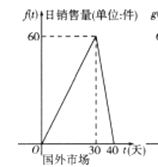 图① 图②
图① 图②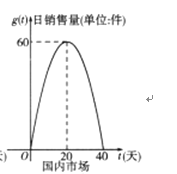
第t天产品广告费用(单位:万元) | 每件产品成本(单位:万元) | 每件产品销售价格(单位:万元) | |
|
| 3 | 6 |
| 10 | 3 | 5 |
(1)分别写出国外市场的日销售量![]() 、国内市场的日销售量
、国内市场的日销售量![]() 与产品上市时间t的函数关系式;
与产品上市时间t的函数关系式;
(2)产品上市后的哪几天,这家公司的日销售利润超过260万元?
(日销售利润=(单件产品销售价-单件产品成本)×日销售量-当天广告费用,![]() )
)
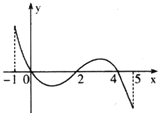
【题目】已知函数![]() 的定义域为
的定义域为![]() ,部分对应值如下表.
,部分对应值如下表.
x |
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
![]() 的导函数
的导函数![]() 的图象如图所示:下列关于
的图象如图所示:下列关于![]() 的命题:
的命题:
![]() 函数
函数![]() 是周期函数;
是周期函数;
![]() 函数
函数![]() 在
在![]() 是减函数;
是减函数;
![]() 如果当
如果当![]() 时,
时,![]() 的最大值是2,那么t的最大值为4;
的最大值是2,那么t的最大值为4;
![]() 函数
函数![]() 的零点个数可能为0、1、2、3、4个.
的零点个数可能为0、1、2、3、4个.
其中正确命题的序号是______.