Question

【题目】如图,在四棱锥中,平面 平面,BC//平面PAD, ,.

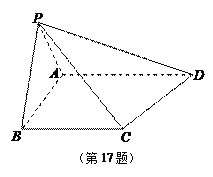
求证:(1) 平面；

(2)平面平面.

Answer 1

【答案】（1）见解析；（2）见解析．

【解析】试题分析：（1）由BC//平面PAD可得BC//AD，根据线面平行的判定定理可得平面；（2）过P作PH AB于H,由条件可得平面，从而可证得BC PH，又BC PB,故有BC 平面PAB，所以平面PBC 平面PAB .

试题解析：

(1)因为BC//平面PAD,

而BC平面ABCD,平面ABCD平面PAD = AD,

所以BC//AD ，

又因为AD 平面PBC,BC平面PBC,

所以平面

(2)过P作PH AB于H,

因为平面 平面,且平面 平面=AB,

所以平面

因为BC 平面ABCD,

所以BC PH.

因为 ,

所以BC PB,

而,

于是点H与B不重合,即PB PH = H.

因为PB,PH 平面PAB,

所以BC 平面PAB

因为BC 平面PBC,

故平面PBC 平面AB.