题目内容
【题目】若![]() ,
,![]() 为自然数
为自然数![]() ,则下列不等式:①
,则下列不等式:①![]() ;②
;②![]() ;③
;③![]() ,其中一定成立的序号是__________.
,其中一定成立的序号是__________.
【答案】①③.
【解析】
对于①根据不等式,作差并构造函数![]() ,利用导数证明函数的单调性即可比较大小;对于不等式②,根据移项变形,构造函数
,利用导数证明函数的单调性即可比较大小;对于不等式②,根据移项变形,构造函数![]() ,通过求
,通过求![]() 即可判断函数的单调性,比较大小即可;对于③,构造函数
即可判断函数的单调性,比较大小即可;对于③,构造函数![]() ,利用换底公式,求导即可判断函数的单调性,进而比较大小即可.
,利用换底公式,求导即可判断函数的单调性,进而比较大小即可.
对于①若![]() 成立.两边同时取对数可得
成立.两边同时取对数可得
![]() ,化简得
,化简得![]()
因为![]()
则![]() ,不等式两边同时除以
,不等式两边同时除以![]() 可得
可得
![]()
令![]() ,
,![]()
则
当![]() 时,
时, ![]() ,所以
,所以![]()
即![]() 在
在![]() 内单调递增
内单调递增
所以当![]() 时
时![]() ,即
,即![]()
所以![]()
故①正确
对于②若![]() ,化简可得
,化简可得![]()
令![]() ,
,![]()
则![]()
由![]() 可知
可知![]() 在
在![]() 内单调递增
内单调递增
而![]()
所以![]() 在
在![]() 内先负后正
内先负后正
因而![]() 在
在![]() 内先递减,再递增,所以当
内先递减,再递增,所以当![]() 时无法判断
时无法判断![]() 与
与![]() 的大小关系.故②错误.
的大小关系.故②错误.
对于③,若![]()
令![]()
利用换底公式化简可得![]() ,
,![]()
则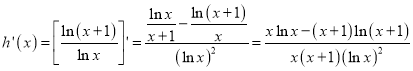
当![]() 时,
时,![]()
所以![]() ,即
,即![]()
则![]() 在
在![]() 内单调递减
内单调递减
所以当![]() 时,
时, ![]()
即![]()
所以③正确
综上可知,正确的为①③
故答案为: ①③

练习册系列答案
相关题目
【题目】为了解使用手机是否对学生的学习有影响,某校随机抽取100名学生,对学习成绩和使用手机情况进行了调查,统计数据如表所示(不完整):
使用手机 | 不使用手机 | 总计 | |
学习成绩优秀 | 10 | 40 | |
学习成绩一般 | 30 | ||
总计 | 100 |
(1)补充完整所给表格,并根据表格数据计算是否有99.9%的把握认为学生的学习成绩与使用手机有关;
(2)现从上表中不使用手机的学生中按学习成绩是否优秀分层抽样选出6人,再从这6人中随机抽取3人,求其中学习成绩优秀的学生恰有2人的概率.
参考公式: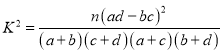 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |