题目内容
9．在等差数列{an}中，a12=33，a22=63，求d和a32．分析 设该数列的首项为a1，公差为d；根据题意可得$\left\{\begin{array}{l}{{a}_{1}+11d=33}\\{{a}_{1}+21d=63}\end{array}\right.$，解可得a1与d的值，由等差数列的通项公式计算可得答案．．
解答 解：根据题意，设该数列的首项为a1，公差为d；
由等差数列{an}中，a12=33，a22=63，可得$\left\{\begin{array}{l}{{a}_{1}+11d=33}\\{{a}_{1}+21d=63}\end{array}\right.$，
解可得$\left\{\begin{array}{l}{{a}_{1}=0}\\{d=3}\end{array}\right.$，
故a32=a1+（32-1）d=93．
点评 本题考查等差数列的通项公式，关键要牢记等差数列的通项公式．
练习册系列答案
相关题目
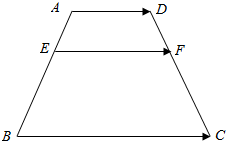如图，在梯形ABCD中，若E，F分别为腰AB，DC的三等分点，且|$\overrightarrow{AD}$|=2，|$\overrightarrow{BC}$|=5，求|$\overrightarrow{EF}$|．
1．在递增等比数列{an}中，a2a16=6，a4+a14=5，则$\frac{{{a_{20}}}}{{{a_{10}}}}$等于（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{2}{3}$或$\frac{3}{2}$ | D． | $-\frac{2}{3}$或$-\frac{3}{2}$ |