题目内容
14.若椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的右焦点F(1,0)与抛物线E:y2=2px(p>0)焦点重合,过F且倾斜角为45°的直线交椭圆于A,B两点,且$\overrightarrow{AF}=3\overrightarrow{FB}$.(1)求椭圆C的方程和抛物线E的方程;
(2)若斜率为k且F的直线l交抛物线E:y2=2px于C、D两点,交椭圆C于M,N两点,问是否存在实常数λ,使$\frac{1}{|MN|}+\frac{λ}{|CD|}$为常数,若存在,求出λ的值;若不存在,说明理由.
分析 (1)由抛物线E:y2=2px(p>0)的焦点与椭圆C的焦点重合,即可求得抛物线方程,再由直线y=x-1代入椭圆方程,运用韦达定理和向量的共线的坐标表示,消去变量,可得a,b的方程,解方程可得椭圆的方程;
(2)依次射出M,N,C,D四点的坐标,设出直线l的方程,联立直线方程和圆锥曲线方程,利用根与系数关系分别写出M,N两点横坐标的和与积,写出C,D两点横坐标的和与积,利用弦长公式求出MN和CD的长度,代入$\frac{1}{|MN|}+\frac{λ}{|CD|}$后,可求出使$\frac{1}{|MN|}+\frac{λ}{|CD|}$为常数的λ的值.
解答 解:(1)F(1,0),即有$\frac{p}{2}$=1,解得p=2,
则抛物线E:y2=4x;
由直线y=x-1代入椭圆方程,可得
(b2+a2)x2-2a2x+a2-a2b2=0,
设A(x1,y1),B(x2,y2),
即有x1+x2=$\frac{2{a}^{2}}{{a}^{2}+{b}^{2}}$,x1x2=$\frac{{a}^{2}-{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$,①
又$\overrightarrow{AF}=3\overrightarrow{FB}$.即有1-x1=3(x2-1),②
联立①②,消去x1,x2,可得a2-a4-a2b2+4b2=0,
又a2-b2=1,解得a2=2,b2=1,
则椭圆C的方程为$\frac{{x}^{2}}{2}$+y2=1;
(2)设M(x1,y1),N(x2,y2),C(x3,y3),D(x4,y4).
直线l的方程为y=k(x-1),与椭圆C的方程联立$\left\{\begin{array}{l}{y=k(x-1)}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$,
得(1+2k2)x2-4k2x+2k2-2=0,
x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$,|MN|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\frac{2\sqrt{2}(1+{k}^{2})}{1+2{k}^{2}}$;
直线l的方程为y=k(x-1),与抛物线G的方程联立$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,
得k2x2-(2k2+4)x+k2=0.x3+x4=$\frac{2{k}^{2}+4}{{k}^{2}}$,
即有|CD|=x3+x4+2=$\frac{4{k}^{2}+4}{{k}^{2}}$.
$\frac{1}{|MN|}+\frac{λ}{|CD|}$=$\frac{1+2{k}^{2}}{2\sqrt{2}(1+{k}^{2})}$+$\frac{λ{k}^{2}}{4(1+{k}^{2})}$=$\frac{\sqrt{2}+(2\sqrt{2}+λ){k}^{2}}{4(1+{k}^{2})}$,
要使$\frac{1}{|MN|}+\frac{λ}{|CD|}$为常数,则$\sqrt{2}$=2$\sqrt{2}$+λ,得λ=-$\sqrt{2}$,
故存在λ=-$\sqrt{2}$,使$\frac{1}{|MN|}+\frac{λ}{|CD|}$为常数$\frac{\sqrt{2}}{4}$.
点评 本题主要考查了曲线方程的求法,考查了直线与圆锥曲线的位置关系的应用,训练了设而不求的解题思想方法,考查了弦长公式的用法,直线与圆锥曲线问题的特点是计算量比较大,要求考生具备较强的运算推理的能力,是难题.

| A. | 一解 | B. | 两解 | C. | 无解 | D. | 解的个数不确定 |
| A. | $\frac{5}{36}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{12}$ |
| A. | $\overrightarrow{ON}$ | B. | $\overrightarrow{AM}$ | C. | $\overrightarrow{AN}$ | D. | 2$\overrightarrow{AN}$ |
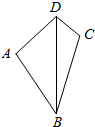 如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.
如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.