题目内容
17.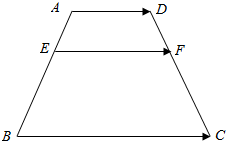 如图,在梯形ABCD中,若E,F分别为腰AB,DC的三等分点,且|$\overrightarrow{AD}$|=2,|$\overrightarrow{BC}$|=5,求|$\overrightarrow{EF}$|.
如图,在梯形ABCD中,若E,F分别为腰AB,DC的三等分点,且|$\overrightarrow{AD}$|=2,|$\overrightarrow{BC}$|=5,求|$\overrightarrow{EF}$|.
分析 如图所示,$\overrightarrow{EF}$=$\overrightarrow{EA}+\overrightarrow{AD}+\overrightarrow{DF}$,$\overrightarrow{EA}=\frac{1}{3}\overrightarrow{BA}$,$\overrightarrow{DF}=\frac{1}{3}\overrightarrow{DC}$.可得$\overrightarrow{EF}$=$\frac{1}{3}\overrightarrow{BA}$+$\overrightarrow{AD}$+$\frac{1}{3}\overrightarrow{DC}$=$\frac{1}{3}\overrightarrow{BC}$+$\frac{2}{3}\overrightarrow{AD}$,再利用数量积运算性质即可得出.
解答 解:如图所示,$\overrightarrow{EF}$=$\overrightarrow{EA}+\overrightarrow{AD}+\overrightarrow{DF}$,$\overrightarrow{EA}=\frac{1}{3}\overrightarrow{BA}$,$\overrightarrow{DF}=\frac{1}{3}\overrightarrow{DC}$.
∴$\overrightarrow{EF}$=$\frac{1}{3}\overrightarrow{BA}$+$\overrightarrow{AD}$+$\frac{1}{3}\overrightarrow{DC}$
=$\frac{1}{3}(\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DC})$+$\frac{2}{3}\overrightarrow{AD}$
=$\frac{1}{3}\overrightarrow{BC}$+$\frac{2}{3}\overrightarrow{AD}$,
∴${\overrightarrow{EF}}^{2}$=$\frac{1}{9}{\overrightarrow{BC}}^{2}+$$\frac{4}{9}\overrightarrow{BC}•\overrightarrow{AD}$+$\frac{4}{9}$${\overrightarrow{AD}}^{2}$
=$\frac{1}{9}×{5}^{2}$+$\frac{4}{9}×2×5$+$\frac{4}{9}×{2}^{2}$
=9.
∴$|\overrightarrow{EF}|$=3.
点评 本题考查了向量共线定理、向量的多边形法则、数量积运算性质,考查了推理能力与计算能力,属于中档题.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案| A. | $\frac{5}{36}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{12}$ |
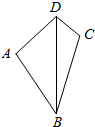 如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.
如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.