题目内容
2.若函数y=3sin(-2x+φ-$\frac{π}{4}$)为偶函数,则φ的取值范围为{φ|φ=kπ+$\frac{3π}{4}$,k∈z }.分析 由条件利用正弦函数、余弦函数的奇偶性,诱导公式可得φ-$\frac{π}{4}$=kπ+$\frac{π}{2}$,k∈z,由此求得φ的取值范围.
解答 解:由函数y=3sin(-2x+φ-$\frac{π}{4}$)为偶函数,可得φ-$\frac{π}{4}$=kπ+$\frac{π}{2}$,k∈z,
求得φ=kπ+$\frac{3π}{4}$,k∈z,
故答案为:{φ|φ=kπ+$\frac{3π}{4}$,k∈z }.
点评 本题主要考查正弦函数、余弦函数的奇偶性,诱导公式,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
10.设函数f(x)=x4-ax(a>0)的零点都在区间[0,5]上,则函数g(x)=$\frac{1}{x}$与函数h(x)=x3-a的图象的交点的横坐标为正整数时,实数a的所有取值中最大值为( )
| A. | $\frac{80}{3}$ | B. | $\frac{255}{4}$ | C. | $\frac{624}{5}$ | D. | $\frac{1295}{6}$ |
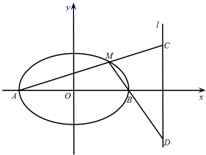 已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,过其右焦点与长轴垂直的弦长为1,如图,A,B是椭圆的左右顶点,M是椭圆上位于x轴上方的动点,直线AM,BM与直线l:x=4分别交于C,D两点.
已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,过其右焦点与长轴垂直的弦长为1,如图,A,B是椭圆的左右顶点,M是椭圆上位于x轴上方的动点,直线AM,BM与直线l:x=4分别交于C,D两点.