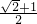题目内容
某地最近出台一项机动车驾照考试规定:每位考试者一年之内最多有4次参加考试的机会,一量某次考试通过,便可领取驾照,不再参加以后的考试,否则就一直考到第4次为止如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9.求在一年内李明参加驾照考试次数ξ的分布列和ξ的期望,并求李明在一所内领到驾照的概率.
解:ξ的取值分别为1,2,3,4.
ξ=1,表明李明第一次参加驾照考试就通过了,
故P(ξ=1)=0.6
ξ=2,表明李明在第一次考试未通过,第二次通过了,
故P(ξ=2)=(1-0.6)×0.7=0.28
ξ=3,表明李明在第一、二次考试未通过,第三次通过了,故
P(ξ=3)=(1-0.6)×(1-0.7)×0.8=0.096.
ξ=4,表明李明在第一、二、三次考试都未通过,故
P(ξ=4)=(1-0.6)×(1-0.7)×(1-0.8)=0.024.
∴李明实际参加考试次数ξ的分布列为
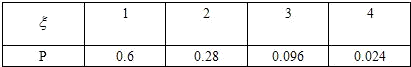
∴ξ的期望Eξ=1×0.6+2×0.28+3×0.096+4×0.024=1.544.李明在一年内领到驾照的概第为
1-(1-0.6)×(1-0.7)×(1-0.8)×(1-0.9)=0.9976.
分析:ξ的取值分别为1,2,3,4.ξ=1,表明李明第一次参加驾照考试就通过了,ξ=2,表明李明在第一次考试未通过,第二次通过了,ξ=3,表明李明在第一、二次考试未通过,第三次通过了,ξ=4,表明李明在第一、二、三次考试都未通过,写出概率,做出期望.
点评:本题这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题.题目的情景和我们的生活比较接近,可以帮助提高学习兴趣.
ξ=1,表明李明第一次参加驾照考试就通过了,
故P(ξ=1)=0.6
ξ=2,表明李明在第一次考试未通过,第二次通过了,
故P(ξ=2)=(1-0.6)×0.7=0.28
ξ=3,表明李明在第一、二次考试未通过,第三次通过了,故
P(ξ=3)=(1-0.6)×(1-0.7)×0.8=0.096.
ξ=4,表明李明在第一、二、三次考试都未通过,故
P(ξ=4)=(1-0.6)×(1-0.7)×(1-0.8)=0.024.
∴李明实际参加考试次数ξ的分布列为
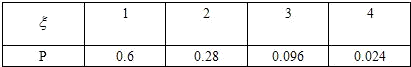
∴ξ的期望Eξ=1×0.6+2×0.28+3×0.096+4×0.024=1.544.李明在一年内领到驾照的概第为
1-(1-0.6)×(1-0.7)×(1-0.8)×(1-0.9)=0.9976.
分析:ξ的取值分别为1,2,3,4.ξ=1,表明李明第一次参加驾照考试就通过了,ξ=2,表明李明在第一次考试未通过,第二次通过了,ξ=3,表明李明在第一、二次考试未通过,第三次通过了,ξ=4,表明李明在第一、二、三次考试都未通过,写出概率,做出期望.
点评:本题这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题.题目的情景和我们的生活比较接近,可以帮助提高学习兴趣.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
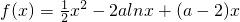 ,a∈R.
,a∈R.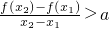 恒成立,若存在求出a的取值范围,若不存在,说明理由.
恒成立,若存在求出a的取值范围,若不存在,说明理由.
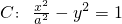 相切,则双曲线C的离心率e=
相切,则双曲线C的离心率e=



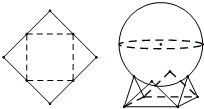 用一个边长为
用一个边长为 的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢.现将半径为1的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为
的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢.现将半径为1的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为