题目内容
直线l1：x=1到直线l2：2x+y+1=0的角是
- A.arctan2，
- B.arctan
- C.π-arctan2
- D.arctan（-）
B
分析：记直线l1到l2的角为α，直线l2的倾斜角为β，作图可见α=β-
，再由tanβ=-2，可求tanα，进而求α．
解答：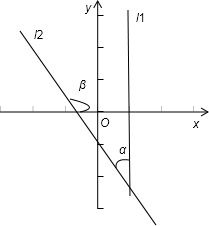
解：记直线l1到l2的角为α，直线l2的倾斜角为β，
作图可见α=β-，tanα=-cotβ=，
故选B．
点评：本题考查一条直线到另一条直线的角，直线的倾斜角的定义，以及诱导公式的应用．
分析：记直线l1到l2的角为α，直线l2的倾斜角为β，作图可见α=β-
，再由tanβ=-2，可求tanα，进而求α．解答：
解：记直线l1到l2的角为α，直线l2的倾斜角为β，作图可见α=β-
，tanα=-cotβ=，故选B．
点评：本题考查一条直线到另一条直线的角，直线的倾斜角的定义，以及诱导公式的应用．
练习册系列答案
相关题目
C.-2 D.
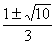(x＋1)
(x＋1)