题目内容
已知(3x+y)2001+x2001+4x+y=0,则4x+y的值为________..
0
分析:结合条件(3x+y)2001+x2001+4x+y=0和要求的结论(4x+y的值)可将条件等价变形为(3x+y)2001+(3x+y)+x2001+x=0,故可构造函数f(x)=x2001+x即可将条件等价变形为f(3x+y)+f(x)=0再结合f(x)的单调性和奇偶性即可解题.
解答:构造函数f(x)=x2001+x,则(3x+y)2001+(3x+y)+x2001+x=0
∴f(3x+y)+f(x)=0
∵f(-x)=-(x2001+x)=-f(x)且定义域为R关于原点对称
∴f(x)的奇函数
∴f(3x+y)=f(-x)
又易得f(x)=x2001+x为R上的单调递增函数
∴3x+y=-x
∴4x+y=0
故答案为0
点评:本题主要考查了函数的单调性和奇偶性.解题的关键是要构造函数f(x)=x2001+x否则此题很难求解.
分析:结合条件(3x+y)2001+x2001+4x+y=0和要求的结论(4x+y的值)可将条件等价变形为(3x+y)2001+(3x+y)+x2001+x=0,故可构造函数f(x)=x2001+x即可将条件等价变形为f(3x+y)+f(x)=0再结合f(x)的单调性和奇偶性即可解题.
解答:构造函数f(x)=x2001+x,则(3x+y)2001+(3x+y)+x2001+x=0
∴f(3x+y)+f(x)=0
∵f(-x)=-(x2001+x)=-f(x)且定义域为R关于原点对称
∴f(x)的奇函数
∴f(3x+y)=f(-x)
又易得f(x)=x2001+x为R上的单调递增函数
∴3x+y=-x
∴4x+y=0
故答案为0
点评:本题主要考查了函数的单调性和奇偶性.解题的关键是要构造函数f(x)=x2001+x否则此题很难求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知变量x,y满足约束条件
,则z=3x+y的最小值为( )
|
| A、2 | B、1 | C、-1 | D、-2 |
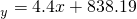 ,则可估计x与y的增长速度之比约为
,则可估计x与y的增长速度之比约为 .
. ,m)三点共线,则m的值为2.
,m)三点共线,则m的值为2.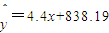 ,则可估计x与y的增长速度之比约为
,则可估计x与y的增长速度之比约为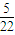 .
. ,m)三点共线,则m的值为2.
,m)三点共线,则m的值为2.