题目内容
已知函数 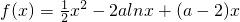 ,a∈R.
,a∈R.
(Ⅰ)当 a=1时,求函数 f(x)的最小值;
(Ⅱ)当a<0时,讨论函数 f(x)的单调性;
(Ⅲ)是否存在实数a,对任意的 x1,x2∈(0,+∞),且x1≠x2,有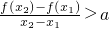 恒成立,若存在求出a的取值范围,若不存在,说明理由.
恒成立,若存在求出a的取值范围,若不存在,说明理由.
解:(Ⅰ)函数f(x)的定义域为(0,+∞),
由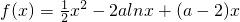 ,
,
当a=1时, ,
,
 .
.
∴当x∈(0,2)时,f'(x)<0,f(x)为减函数;
当x∈(2,+∞),f'(x)>0,f(x)为增函数.
∴f(x)在x=2时取得最小值,其最小值为f(2)=-2ln2.
(Ⅱ)∵ ,
,
∴(1)当-2<a<0时,若x∈(0,-a),f'(x)>0,f(x)为增函数;
若x∈(-a,2),f'(x)<0,f(x)为减函数;
若x∈(2,+∞),f'(x)>0,f(x)为增函数.
(2)当a=-2时,在(0,+∞)上f′(x)≥0,f(x)为增函数;
(3)当a<-2时,若x∈(0,2),f'(x)>0,f(x)为增函数;
若x∈(2,-a),f'(x)<0,f(x)为减函数;
若x∈(-a,+∞),f'(x)>0,f(x)为增函数.
(Ⅲ)假设存在实数a使得对任意的 x1,x2∈(0,+∞),且x1≠x2,有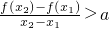 恒成立,
恒成立,
不妨设0<x1<x2,只要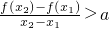 ,即:f(x2)-ax2>f(x1)-ax1.
,即:f(x2)-ax2>f(x1)-ax1.
令g(x)=f(x)-ax,只要 g(x)在(0,+∞)为增函数即可.
又函数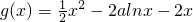 .
.
考查函数
要使g'(x)≥0在(0,+∞)恒成立,只要-1-2a≥0,即a ,
,
故存在实数a ,对任意的 x1,x2∈(0,+∞),且x1≠x2,
,对任意的 x1,x2∈(0,+∞),且x1≠x2,
有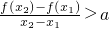 恒成立.
恒成立.
分析:(Ⅰ)把a=1代入函数解析式,求导后解出导函数的零点,由导函数的零点对定义域分段,判出在各区间段内的单调性,从而的导函数的最小值;
(Ⅱ)求出函数的导函数,根据a的不同取值对函数定义域分段,由函数导函数的符号判断原函数在各区间段内的单调性;
(Ⅲ)在假设存在实数a使得对任意的 x1,x2∈(0,+∞),且x1≠x2,有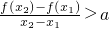 恒成立的前提下,把问题转化为(x2)-ax2>f(x1)-ax1恒成立,然后构造函数g(x)=f(x)-ax,利用导函数求出使函数g(x)在(0,+∞)上为增函数的a的取值范围.
恒成立的前提下,把问题转化为(x2)-ax2>f(x1)-ax1恒成立,然后构造函数g(x)=f(x)-ax,利用导函数求出使函数g(x)在(0,+∞)上为增函数的a的取值范围.
点评:本题考查了利用导数研究函数的单调性,考查了导数在最大值最小值中的应用,考查了数学转化思想和分类讨论的数学思想方法,训练了利用构造函数法求参数的取值范围,属难题.
由
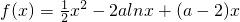 ,
,当a=1时,
 ,
, .
.∴当x∈(0,2)时,f'(x)<0,f(x)为减函数;
当x∈(2,+∞),f'(x)>0,f(x)为增函数.
∴f(x)在x=2时取得最小值,其最小值为f(2)=-2ln2.
(Ⅱ)∵
 ,
,∴(1)当-2<a<0时,若x∈(0,-a),f'(x)>0,f(x)为增函数;
若x∈(-a,2),f'(x)<0,f(x)为减函数;
若x∈(2,+∞),f'(x)>0,f(x)为增函数.
(2)当a=-2时,在(0,+∞)上f′(x)≥0,f(x)为增函数;
(3)当a<-2时,若x∈(0,2),f'(x)>0,f(x)为增函数;
若x∈(2,-a),f'(x)<0,f(x)为减函数;
若x∈(-a,+∞),f'(x)>0,f(x)为增函数.
(Ⅲ)假设存在实数a使得对任意的 x1,x2∈(0,+∞),且x1≠x2,有
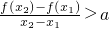 恒成立,
恒成立,不妨设0<x1<x2,只要
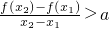 ,即:f(x2)-ax2>f(x1)-ax1.
,即:f(x2)-ax2>f(x1)-ax1.令g(x)=f(x)-ax,只要 g(x)在(0,+∞)为增函数即可.
又函数
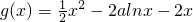 .
.考查函数

要使g'(x)≥0在(0,+∞)恒成立,只要-1-2a≥0,即a
 ,
,故存在实数a
 ,对任意的 x1,x2∈(0,+∞),且x1≠x2,
,对任意的 x1,x2∈(0,+∞),且x1≠x2,有
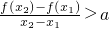 恒成立.
恒成立.分析:(Ⅰ)把a=1代入函数解析式,求导后解出导函数的零点,由导函数的零点对定义域分段,判出在各区间段内的单调性,从而的导函数的最小值;
(Ⅱ)求出函数的导函数,根据a的不同取值对函数定义域分段,由函数导函数的符号判断原函数在各区间段内的单调性;
(Ⅲ)在假设存在实数a使得对任意的 x1,x2∈(0,+∞),且x1≠x2,有
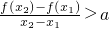 恒成立的前提下,把问题转化为(x2)-ax2>f(x1)-ax1恒成立,然后构造函数g(x)=f(x)-ax,利用导函数求出使函数g(x)在(0,+∞)上为增函数的a的取值范围.
恒成立的前提下,把问题转化为(x2)-ax2>f(x1)-ax1恒成立,然后构造函数g(x)=f(x)-ax,利用导函数求出使函数g(x)在(0,+∞)上为增函数的a的取值范围.点评:本题考查了利用导数研究函数的单调性,考查了导数在最大值最小值中的应用,考查了数学转化思想和分类讨论的数学思想方法,训练了利用构造函数法求参数的取值范围,属难题.

练习册系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0).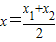 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. ,a∈R.
,a∈R. 上的任意一个x,都有f(x)≤1成立,求a的取值范围.
上的任意一个x,都有f(x)≤1成立,求a的取值范围. (a∈R).
(a∈R). 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
 .
.