题目内容
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的长半轴为半径的圆与直线
的长半轴为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,
, ![]() 为动直线
为动直线![]() 与椭圆
与椭圆![]() 的两个交点,问:在
的两个交点,问:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为定值?若存在,试求出点
为定值?若存在,试求出点![]() 的坐标和定值,若不存在,请说明理由.
的坐标和定值,若不存在,请说明理由.
【答案】(1)![]() ;(2)定点为
;(2)定点为![]() ,
, ![]() .
.
【解析】试题分析:(Ⅰ)由e=![]() ,以原点O为圆心,椭圆C的长半轴长为半径的圆与直线
,以原点O为圆心,椭圆C的长半轴长为半径的圆与直线![]() 相切,求出a,b,由此能求出椭圆的方程.
相切,求出a,b,由此能求出椭圆的方程.
(Ⅱ)由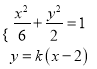 ,得(1+3k2)x2﹣12k2x+12k2﹣6=0,由此利用韦达定理、向量的数量积,结合已知条件能求出在x轴上存在点E,使
,得(1+3k2)x2﹣12k2x+12k2﹣6=0,由此利用韦达定理、向量的数量积,结合已知条件能求出在x轴上存在点E,使![]() 为定值,定点为(
为定值,定点为(![]() ).
).
试题解析:
(Ⅰ)由e=![]() ,得
,得![]() =
=![]() ,即c=
,即c=![]() a,①
a,①
以原点O为圆心,椭圆C的长半轴长为半径的圆为x2+y2=a2,
此圆与直线2x﹣![]() +6=0相切,∴a=
+6=0相切,∴a=![]() =
=![]() ,
,
代入①得c=2,(4分)
∴b2=a2﹣c2=2,∴椭圆的方程为![]() .
.
(Ⅱ)由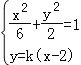 ,得(1+3k2)x2﹣12k2x+12k2﹣6=0,(6分)
,得(1+3k2)x2﹣12k2x+12k2﹣6=0,(6分)
设A(x1,y1),B(x2,y2),∴![]() ,
,![]() ,
,
根据题意,假设x轴上存在定点E(m,0),使得![]() 为定值,
为定值,
则有![]() =(x1﹣m,y1)(x2﹣m,y2)=(x1﹣m)(x2﹣m)+y1y2
=(x1﹣m,y1)(x2﹣m,y2)=(x1﹣m)(x2﹣m)+y1y2
=![]()
=(k2+1)![]()
=(k2+1)![]() ﹣(2k2+m)
﹣(2k2+m)![]() +(4k2+m2)
+(4k2+m2)
=![]() ,
,
要使上式为定值,即与k无关,则应有3m2﹣12m+10=3(m2﹣6),
即m=![]() ,此时
,此时![]() =
=![]() 为定值,定点为(
为定值,定点为(![]() ).
).

【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过3S微克/立方米,
的年平均浓度不得超过3S微克/立方米, ![]() 的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天
的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天![]() 的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
组别 |
| 频数(天) | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
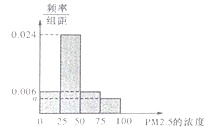
(Ⅰ)将这20天的测量结果按表中分组方法绘制成的样本频率分布直方图如图.
(ⅰ)求图中![]() 的值;
的值;
(ⅱ)在频率分布直方图中估算样本平均数,并根据样本估计总体的思想,从![]() 的年平均度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
的年平均度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
(Ⅱ)将频率视为概率,对于2016年的某3天,记这3天中该居民区![]() 的24小时平均浓度符合环境空气质量标准的天数为
的24小时平均浓度符合环境空气质量标准的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,将木兰溪流经市区河段分成![]() 段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如下表:
段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如下表:
南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
(Ⅰ)记评分在![]() 以上(包括
以上(包括![]() )为优良,从中任取一段,求在同一段中两岸环保评分均为优良的概率;
)为优良,从中任取一段,求在同一段中两岸环保评分均为优良的概率;
(Ⅱ)根据表中数据完成下面茎叶图;
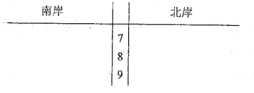
(Ⅲ)分别估计两岸分值的中位数,并计算它们的平均值,试从计算结果分析两岸环保情况,哪边保护更好.
【题目】已知函数f(x)=![]() sinωxcosωx-cos2ωx+
sinωxcosωx-cos2ωx+![]() (ω>0),经化简后利用“五点法”画其在某一周期内的图象时,列表并填入的部分数据如下表:
(ω>0),经化简后利用“五点法”画其在某一周期内的图象时,列表并填入的部分数据如下表:
x | ① |
|
| ||
f(x) | 0 | 1 | 0 | -1 | 0 |
(1)请直接写出①处应填的值,并求函数f(x)在区间![]() 上的值域;
上的值域;
(2)△ABC的内角A,B,C所对的边分别为a,b,c,已知f(A+![]() )=1,b+c=4,a=
)=1,b+c=4,a=![]() ,求△ABC的面积.
,求△ABC的面积.