题目内容
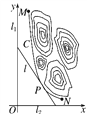
【题目】已知椭圆G： 
的离心率为
，过椭圆G右焦点F的直线m：x＝1与椭圆G交于点M(点M在第一象限)．
(Ⅰ)求椭圆G的方程；
(Ⅱ)已知A为椭圆G的左顶点，平行于AM的直线l与椭圆G相交于B，C两点，请判断直线MB，MC是否关于直线m对称，并说明理由．
【答案】(Ⅰ) 
；(Ⅱ)直线MB，MC关于直线m对称，理由见解析.
【解析】试题分析：（Ⅰ）由已知条件推导出c=1， 
，由此能求出椭圆的方程．
（Ⅱ）由已知条件得A(－2,0)，M(1， 
)，设直线l: 
，n≠1．设B（x1，y1），C（x2，y2），由
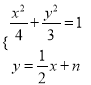，得x2+nx+n2﹣3=0．再由根的判别式和韦达定理结合已知条件能求出直线MB，MC关于直线m对称．
试题解析：
(Ⅰ)由题意得c＝1,
由
＝
可得a＝2，
所以b2＝a2－c2＝3,
所以椭圆的方程为
＋
＝1.
(Ⅱ)由题意可得点A(－2,0)，M(1，
)，
所以由题意可设直线l：y＝x＋n，n≠1.
设B(x1，y1)，C(x2，y2)，
由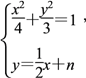
得x2＋nx＋n2－3＝0.
由题意可得Δ＝n2－4(n2－3)＝12－3n2>0，即n∈(－2,2)且n≠1.
x1＋x2＝－n，x1x2＝n2－3
因为kMB＋kMC＝
＋
＝
＋
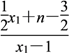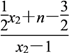
＝1＋
＋
＝1＋
＝1－
＝0，
所以直线MB，MC关于直线m对称.
练习册系列答案
相关题目
