题目内容
19.求函数f(x)=$\frac{{x}^{2}-2x+3}{x}$(x<0)的最大值及取得最大值时x的值.分析 f(x)可化为f(x)=x+$\frac{3}{x}$-2=-[(-x)+$\frac{3}{-x}$]-2,由基本不等式,即可得到最大值及对应的x的值.
解答 解:因为x<0,
所以f(x)=$\frac{{x}^{2}-2x+3}{x}$
=x+$\frac{3}{x}$-2=-[(-x)+$\frac{3}{-x}$]-2
≤-2$\sqrt{(-x)•\frac{3}{-x}}$-2=-2$\sqrt{3}$-2,
当且仅当x=-$\sqrt{3}$时,取得最大值-2$\sqrt{3}$-2.
点评 本题考查函数的最值的求法,注意运用基本不等式,以及满足的条件:一正二定三等,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知等差数列{an}中,a4+a7=42,则前10项和S10=( )
| A. | 420 | B. | 380 | C. | 210 | D. | 140 |
2.在△ABC中,若2cosB•sinA=sinC,则△ABC一定是( )三角形.
| A. | 等腰 | B. | 直角 | C. | 等边 | D. | 等腰直角 |
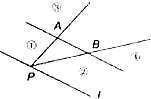 如图,点P是直线l上一点,l∥直线AB,如果存在实数x,y,使得$\overrightarrow{PC}=x\overrightarrow{PA}+y\overrightarrow{PB}$,且x+y=2,x>2,则点C所在的区域是图中标示的区域( )
如图,点P是直线l上一点,l∥直线AB,如果存在实数x,y,使得$\overrightarrow{PC}=x\overrightarrow{PA}+y\overrightarrow{PB}$,且x+y=2,x>2,则点C所在的区域是图中标示的区域( )