题目内容
7.已知函数f(x)=$\left\{\begin{array}{l}{x+a,x≤1}\\{\frac{x-1}{{x}^{2}+1},x>1}\end{array}\right.$,问a为何值时,$\underset{lim}{x→1}$f(x)存在.分析 f(x)为分段函数,可以看出$\underset{lim}{x→1}f(x)$存在时,需满足$\underset{lim}{x→1}f(x)=f(1)$,这样求出$\underset{lim}{x→{1}^{+}}f(x)$即可得出a的值.
解答 解:f(1)=1+a,则$\underset{lim}{x→1}f(x)$存在时:
$\underset{lim}{x→{1}^{+}}\frac{x-1}{{x}^{2}+1}=0=1+a$;
∴a=-1;
即a=-1时,$\underset{lim}{x→1}f(x)$存在.
点评 考查函数极限的概念,分段函数极限的求法,以及函数的左右极限的定义及求法,清楚f(x)在x0有定义时,$\underset{lim}{x→{x}_{0}}f(x)$存在的充要条件.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
17.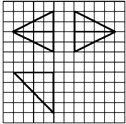 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{6}$ | C. | 4$\sqrt{2}$ | D. | 4$\sqrt{3}$ |