题目内容
数列{an}中,an=-2n2+29n+3,则此数列最大项的值是( )
| A.103 | B.108 | C.103 | D.108 |
D
根据题意结合二次函数的性质可得:
an=-2n2+29n+3=-2(n2-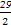 n)+3
n)+3
=-2(n-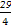 )2+3+
)2+3+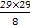 .
.
∴n=7时,a7=108为最大值.
an=-2n2+29n+3=-2(n2-
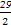 n)+3
n)+3=-2(n-
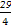 )2+3+
)2+3+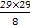 .
.∴n=7时,a7=108为最大值.

练习册系列答案
相关题目
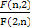 (n∈N*),若对任意正整数n,都有an≥ak(k∈N*)成立,则ak的值为( )
(n∈N*),若对任意正整数n,都有an≥ak(k∈N*)成立,则ak的值为( )
 的前
的前 项积记为
项积记为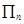 ,若
,若 ,则
,则 ( )
( )



