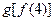题目内容
对函数y=f(x)定义域中任一个x的值均有f(x+a)=f(a-x),
(1)求证y=f(x)的图像关于直线x=a对称;
(2)若函数f(x)对一切实数x都有f(x+2)=f(2-x),且方程f(x)=0恰好有四个不同实根,求这些实根之和。
(1)求证y=f(x)的图像关于直线x=a对称;
(2)若函数f(x)对一切实数x都有f(x+2)=f(2-x),且方程f(x)=0恰好有四个不同实根,求这些实根之和。
(1) 证明略(2) f(x)=0的四根之和为8
设(x0,y0)是函数y=f(x)图像上任一点,则y0=f(x0),
∵ =a, ∴点(x0,y0)与(2a-x0,y0)关于直线x=a对称,
=a, ∴点(x0,y0)与(2a-x0,y0)关于直线x=a对称,
又f(a+x)=f(a-x),
∴f(2a-x0)=f[a+(a-x0)]=f[a-(a-x0)]=f(x0)=y0,
∴(2a-x0,y0)也在函数的图像上,
故y=f(x)的图像关于直线x=a对称.
(2)解:由f(2+x)=f(2-x)得y=f(x)的图像关于直线x=2对称,
若x0是f(x)=0的根,则4-x0也是f(x)=0的根,
若x1是f(x)=0的根,则4-x1也是f(x)=0的根,
∴x0+(4-x0)+ x1+(4-x1)=8
即f(x)=0的四根之和为8.
∵
 =a, ∴点(x0,y0)与(2a-x0,y0)关于直线x=a对称,
=a, ∴点(x0,y0)与(2a-x0,y0)关于直线x=a对称,又f(a+x)=f(a-x),
∴f(2a-x0)=f[a+(a-x0)]=f[a-(a-x0)]=f(x0)=y0,
∴(2a-x0,y0)也在函数的图像上,
故y=f(x)的图像关于直线x=a对称.
(2)解:由f(2+x)=f(2-x)得y=f(x)的图像关于直线x=2对称,
若x0是f(x)=0的根,则4-x0也是f(x)=0的根,
若x1是f(x)=0的根,则4-x1也是f(x)=0的根,
∴x0+(4-x0)+ x1+(4-x1)=8
即f(x)=0的四根之和为8.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的观光带AB,同时建一条连接观光带和湖岸的长为2
的观光带AB,同时建一条连接观光带和湖岸的长为2
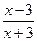
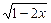 的值域是( )
的值域是( )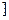
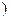
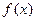 是定义在
是定义在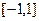 上的奇函数,且
上的奇函数,且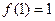 ,若
,若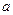 、
、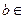
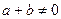 ,有
,有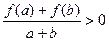 ;
;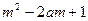 对所有的
对所有的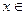
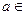
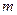 的取值范围。
的取值范围。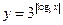 的图象大致是
的图象大致是
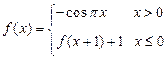 ,则
,则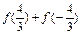 的值等于
的值等于 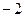
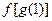 相同的是( )
相同的是( )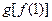 ;
;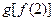 ;
;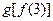 ;
;