题目内容
若函数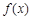 为定义域
为定义域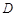 上单调函数,且存在区间
上单调函数,且存在区间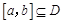 (其中
(其中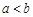 ),使得当
),使得当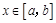 时,
时,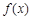 的值域恰为
的值域恰为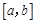 ,则称函数
,则称函数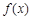 是
是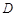 上的正函数,区间
上的正函数,区间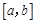 叫做等域区间.如果函数
叫做等域区间.如果函数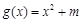 是
是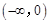 上的正函数,则实数
上的正函数,则实数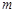 的取值范围为 ▲ .
的取值范围为 ▲ .
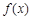 为定义域
为定义域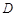 上单调函数,且存在区间
上单调函数,且存在区间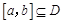 (其中
(其中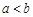 ),使得当
),使得当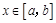 时,
时,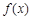 的值域恰为
的值域恰为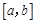 ,则称函数
,则称函数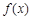 是
是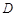 上的正函数,区间
上的正函数,区间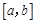 叫做等域区间.如果函数
叫做等域区间.如果函数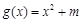 是
是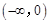 上的正函数,则实数
上的正函数,则实数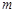 的取值范围为 ▲ .
的取值范围为 ▲ .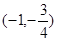
根据函数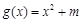 是
是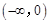 上的正函数建立方程组,消去
上的正函数建立方程组,消去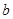 ,求出
,求出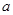 的取值范围,转化成关于
的取值范围,转化成关于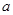 的方程
的方程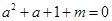 在区间
在区间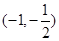 内有实数解进行求解。
内有实数解进行求解。
因为函数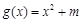 是
是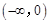 上为减函数,所以当
上为减函数,所以当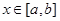 时,
时,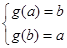
即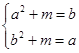 ,两式相减得,
,两式相减得,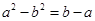 ,即
,即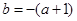 ,代入
,代入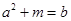 得
得
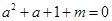 ,由
,由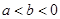 ,且
,且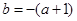 ,得
,得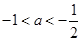
故关于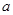 的方程
的方程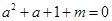 在区间
在区间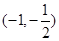 内有实数解
内有实数解
记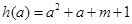 ,则
,则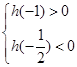 ,解得
,解得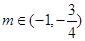
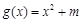 是
是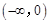 上的正函数建立方程组,消去
上的正函数建立方程组,消去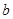 ,求出
,求出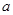 的取值范围,转化成关于
的取值范围,转化成关于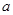 的方程
的方程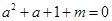 在区间
在区间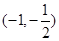 内有实数解进行求解。
内有实数解进行求解。因为函数
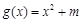 是
是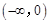 上为减函数,所以当
上为减函数,所以当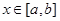 时,
时,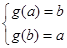
即
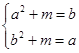 ,两式相减得,
,两式相减得,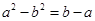 ,即
,即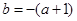 ,代入
,代入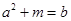 得
得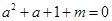 ,由
,由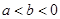 ,且
,且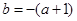 ,得
,得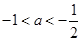
故关于
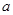 的方程
的方程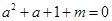 在区间
在区间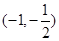 内有实数解
内有实数解记
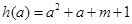 ,则
,则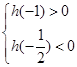 ,解得
,解得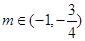

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
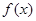 在
在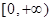 上是增函数,
上是增函数,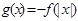 ,若
,若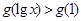 ,则
,则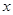 的取值范围是
的取值范围是 
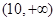
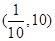

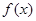 对任意实数
对任意实数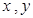 都有
都有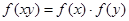 ,且
,且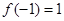 ,
,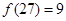
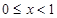 时,
时,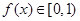 .
.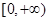 上的单调性,并给出证明;若
上的单调性,并给出证明;若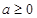 ,且
,且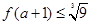 ,求
,求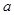 的取值范围.
的取值范围.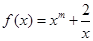 且
且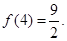
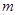 的值;(2)判定
的值;(2)判定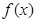 的奇偶性;
的奇偶性;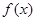 定义在
定义在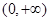 上,
上,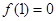 ,导函数
,导函数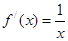 ,
,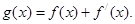
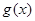 与
与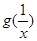 的大小关系;
的大小关系;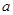 的取值范围,使得
的取值范围,使得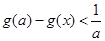 对任意
对任意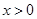 成立.
成立.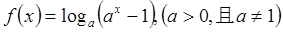 ,
,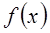 的定义域; (2)讨论函数
的定义域; (2)讨论函数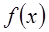 的单调性。
的单调性。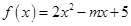 ,
,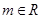 ,它在
,它在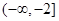 上单调递减,则
上单调递减,则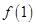 的取值范围是 ( )
的取值范围是 ( )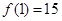
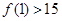

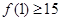
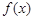 是定义在
是定义在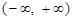 上的偶函数. 当
上的偶函数. 当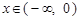 时,
时,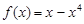 ,
,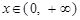 时,
时, .
.