题目内容
.(本小题满分12分)设函数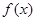 定义在
定义在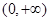 上,
上,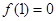 ,导函数
,导函数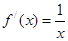 ,
,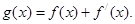
(I)讨论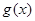 与
与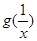 的大小关系;
的大小关系;
(II)求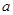 的取值范围,使得
的取值范围,使得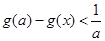 对任意
对任意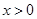 成立.
成立.
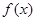 定义在
定义在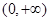 上,
上,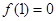 ,导函数
,导函数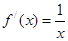 ,
,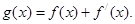
(I)讨论
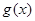 与
与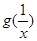 的大小关系;
的大小关系;(II)求
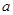 的取值范围,使得
的取值范围,使得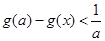 对任意
对任意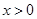 成立.
成立.解:(I)∵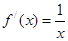 ,∴
,∴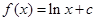 (c为常数),又∵
(c为常数),又∵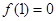 ,所以
,所以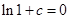 ,即
,即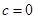 ,∴
,∴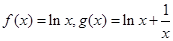 ,∴
,∴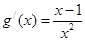 ,
,
令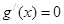 得
得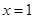 ,
,
当x∈(0,1)时,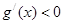 ,
,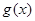 是减函数,故(0,1)是
是减函数,故(0,1)是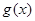 的单调减区间。
的单调减区间。
当x∈(1,+∞)时, ,
,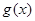 是增函数,故(1,+∞)是
是增函数,故(1,+∞)是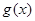 的单调递增区间,
的单调递增区间,
因此,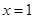 是
是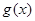 的唯一极值点,且为极小值点,从而是最小值点,
的唯一极值点,且为极小值点,从而是最小值点,
所以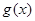 的最小值为
的最小值为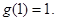
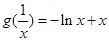 ,设
,设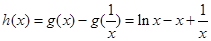 ,则
,则 ,
,
当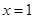 时,
时,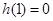 ,即
,即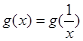 .
.
当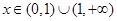 时,
时,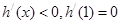 ,因此,
,因此,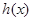 在
在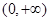 内单调递减,
内单调递减,
当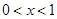 时,
时, ,即
,即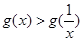 ;
;
当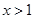 时,
时,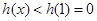 ,即
,即
(II)由(I)知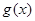 的最小值为1,所以,
的最小值为1,所以,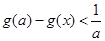 ,对任意
,对任意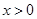 成立
成立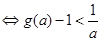 ,即
,即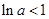 ,从而得
,从而得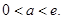
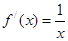 ,∴
,∴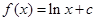 (c为常数),又∵
(c为常数),又∵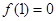 ,所以
,所以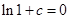 ,即
,即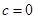 ,∴
,∴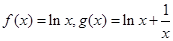 ,∴
,∴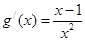 ,
,令
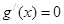 得
得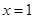 ,
,当x∈(0,1)时,
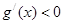 ,
,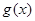 是减函数,故(0,1)是
是减函数,故(0,1)是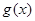 的单调减区间。
的单调减区间。当x∈(1,+∞)时,
 ,
,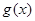 是增函数,故(1,+∞)是
是增函数,故(1,+∞)是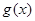 的单调递增区间,
的单调递增区间,因此,
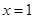 是
是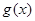 的唯一极值点,且为极小值点,从而是最小值点,
的唯一极值点,且为极小值点,从而是最小值点,所以
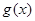 的最小值为
的最小值为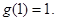
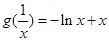 ,设
,设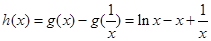 ,则
,则 ,
,当
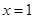 时,
时,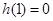 ,即
,即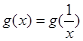 .
.当
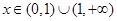 时,
时,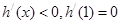 ,因此,
,因此,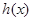 在
在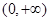 内单调递减,
内单调递减,当
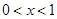 时,
时, ,即
,即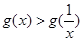 ;
;当
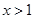 时,
时,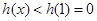 ,即
,即
(II)由(I)知
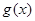 的最小值为1,所以,
的最小值为1,所以,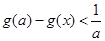 ,对任意
,对任意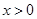 成立
成立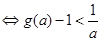 ,即
,即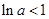 ,从而得
,从而得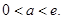
略

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
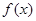 的定义域为
的定义域为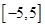 .若当
.若当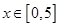 时,
时, 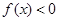 的解集是 .
的解集是 .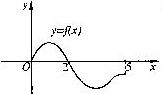
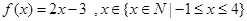 ,则函数的值域为___
,则函数的值域为___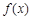 为定义域
为定义域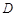 上单调函数,且存在区间
上单调函数,且存在区间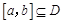 (其中
(其中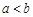 ),使得当
),使得当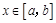 时,
时,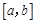 ,则称函数
,则称函数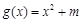 是
是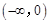 上的正函数,则实数
上的正函数,则实数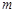 的取值范围为 ▲ .
的取值范围为 ▲ .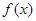 的最小正周期为
的最小正周期为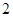 ,并且
,并且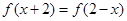 对一切实数
对一切实数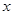 恒成立,则
恒成立,则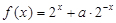 是定义域为
是定义域为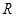 的奇函数,(1)求实数
的奇函数,(1)求实数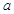 的值;(2)证明
的值;(2)证明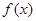 是
是 ,不等式
,不等式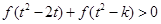 恒成立,求
恒成立,求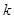 的取值范围。
的取值范围。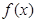 在R上是奇函数,且
在R上是奇函数,且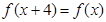 ,当
,当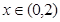 时,
时,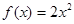 时,则
时,则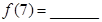 .
.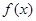 是偶函数,在(-∞,0]上是减函数,则满足
是偶函数,在(-∞,0]上是减函数,则满足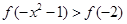 的x的取值范围是
的x的取值范围是 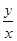 的最大值为 ■
的最大值为 ■