题目内容
已知圆的方程x2+y2=25,点A为该圆上的动点,AB与x轴垂直,B为垂足,点P分有向线段BA的比λ=
.
(1)求点P的轨迹方程并化为标准方程形式;
(2)写出轨迹的焦点坐标和准线方程.
| 3 |
| 2 |
(1)求点P的轨迹方程并化为标准方程形式;
(2)写出轨迹的焦点坐标和准线方程.
(1)设点P(x,y)是轨迹上任意一点,点A的坐标是(x1,y1),点B的坐标是(x1,0),
∵点P分有向线段BA的比λ=
,
∴
,∴
,
又点A在圆x2+y2=25上,∴x2+
y2=25,
即
+
=1(y≠0);
(2)由椭圆
+
=1,知a2=25,b2=9,
∴c=4,则椭圆
+
=1的焦点坐标是(-4,0),(4,0),准线方程是x=±
=±
.
∵点P分有向线段BA的比λ=
| 3 |
| 2 |
∴
|
|
又点A在圆x2+y2=25上,∴x2+
| 25 |
| 9 |
即
| x2 |
| 25 |
| y2 |
| 9 |
(2)由椭圆
| x2 |
| 25 |
| y2 |
| 9 |
∴c=4,则椭圆
| x2 |
| 25 |
| y2 |
| 9 |
| a2 |
| c |
| 25 |
| 4 |

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
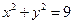 和
和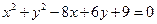 的位置关系是( )
的位置关系是( )